简单的线性规划问题

简单的线性规划问题在高中数学里体现了数形结合的思想方法，特别是线性规划中的参数问题是考试重点与难点之一，因此根据教学体会，写出一点解线性规划问题方法，希望能给同学们有一点小帮助。

一、二元一次不等式组表示的平面区域

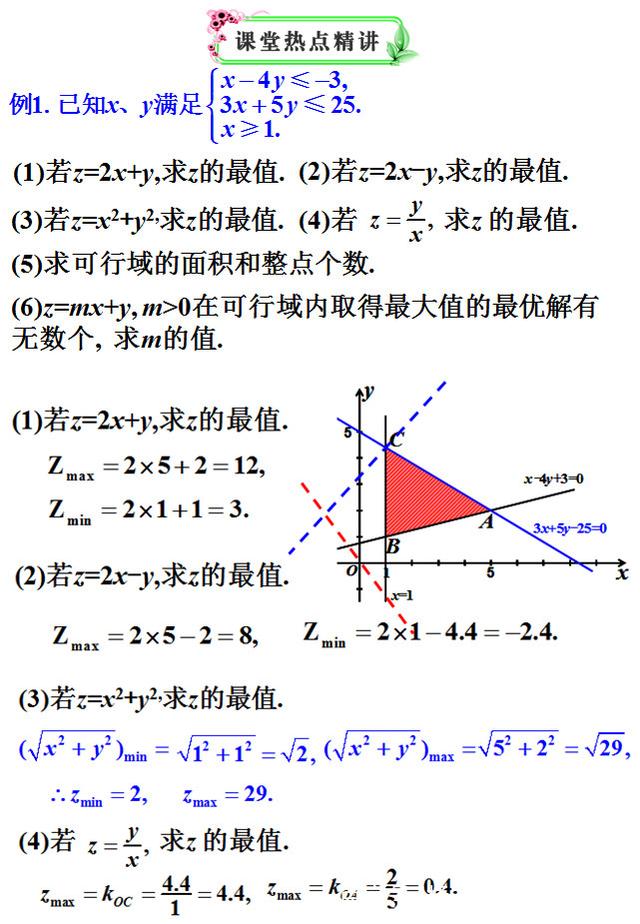
（1）一般地，二元一次不等式Ax＋By＋C>0在平面直角坐标系中表示直线Ax＋By＋C＝0某一侧所有点组成的平面区域。我们把直线画成虚线以表示区域不包括边界直线。当我们在坐标系中画不等式Ax＋By＋C≥0所表示的平面区域时，此区域应包括边界直线，则把边界直线画成实线。

（2）由于对直线Ax＋By＋C＝0同一侧的所有点(x，y)，把它的坐标(x，y)代入Ax＋By＋C，所得的符号都相同，所以只需在此直线的同一侧取一个特殊点(x0，y0)作为测试点，由Ax0＋By0＋C的符号即可判断Ax＋By＋C>0表示的直线是在Ax＋By＋C＝0哪一侧的平面区域。

（1）

【方法总结】

确定二元一次不等式(组)表示的平面区域的方法：

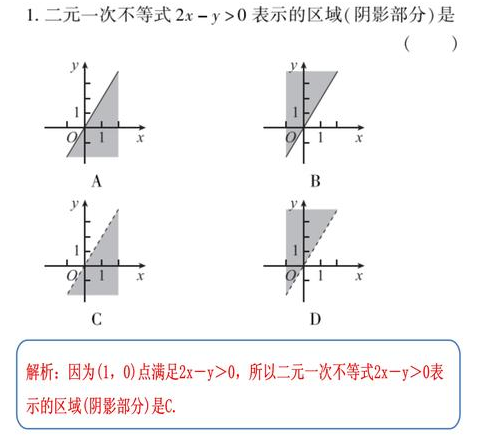
（1）“直线定界，特殊点定域”，即选作直线，再取特殊点并代入不等式组，若满足不等式组，则不等式(组)表示的平面区域为直线与特殊点同侧的那部分区域；否则就对应与特殊点异侧的平面区域．若直线不过原点，特殊点一般取(0，0)点。

（2）当不等式中带等号时，边界为实线，不带等号时，边界应画为虚线，特殊点常取原点。

二、目标函数的最值问题

（2）

解决线性规划问题的主要方法策略：

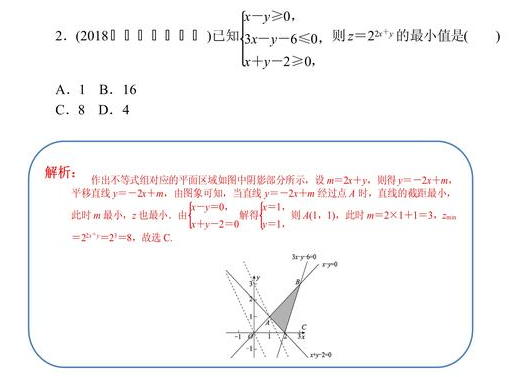
（1）截距法：作出线性约束条件表示的平面区域，将线性目标函数对应的直线方程化为斜截式，再将截距变为0得到过原点的直线，平移此直线使之始终保持与平面区域有公共点，截距的最值即为线性目标函数的最值。此种方法是最常见的解决线性规划问题的策略，对平面区域作图以及线性目标函数对应直线相对于平面区域边界直线的倾斜程度的准确性要求较高。

（2）顶点法：如果可行域是一个多边形围成的区域(包括边界多边形)时，线性目标函数z＝f(x，y)的最优解一般在多边形的顶点处取到，排除在边界处取到的情况，先分别计算出线性目标函数z＝f(x，y)在各个顶点处的函数值，再比较大小即可。

三、线性规划中的参数问题

（3）

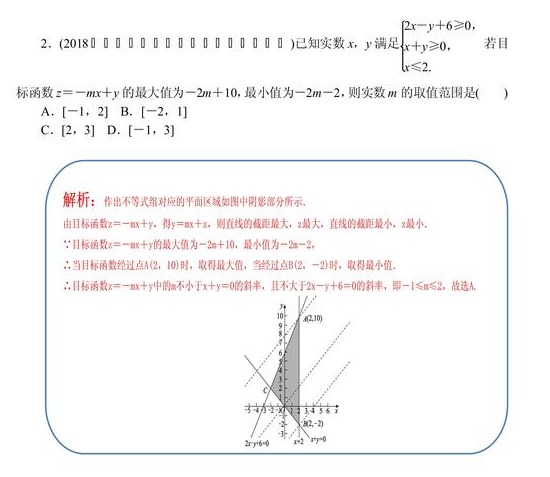
求解线性规划中含参数问题的方法：

（1）若限制条件中含参数，依据参数的不同范围将各种情况下的可行域画出来，寻求最优解，确定参数的值；

（2）若线性目标函数中含有参数，可对线性目标函数的斜率分类讨论，以此来确定线性目标函数经过哪个顶点取得最值，从而求出参数的值；也可以直接求出线性目标函数经过各顶点时对应的参数的值，然后进行检验，找出符合题意的参数值。

---------------------

今天方法君给大家整理一下线性规划的内容，这是解析几何的重点。但是这块内容高考只考察5分，一般以选填的情况出现，难度不大。同学们需要的是细心，以及熟练掌握直线的相关性质。

线性规划

来源：http://www.sohu.com/a/249140600_100250056

------------------

线性规划是数形结合的体现

线性规划实质上是“数形结合”数学思想方法在一个方面的体现，将最值问题借助图形直观、简便地寻找出来，是一种较快地求最值的方法。在求解应用问题时要特别注意题目中的变量的取值范围，不可将范围盲目扩大．

探究提高

本题主要考查不等式表示的平面区域、数列求和及不等式的应用等基础知识，考查了数形结合的方法和逻辑推理能力．

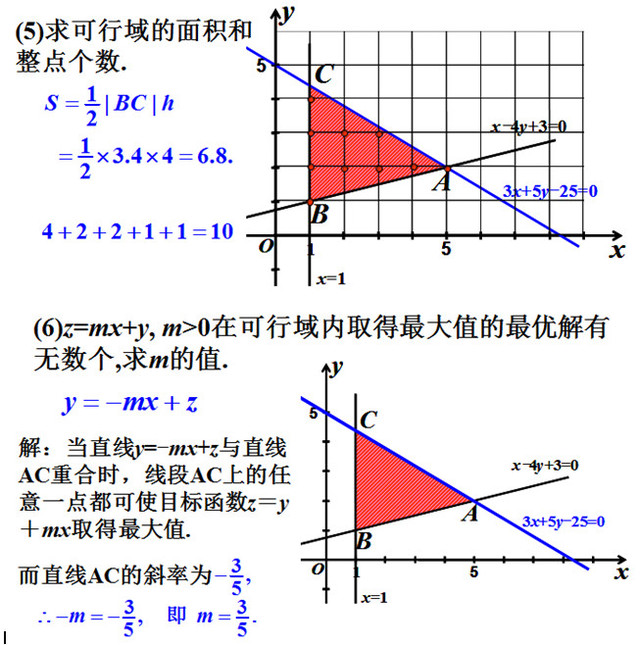
不等式组表示的平面区域是各个不等式所表示的平面区域点集的交集，因而是各个不等式所表示的平面区域的公共部分．在封闭区域内找整点数目时，若数目较小时，可画网格逐一数出；若数目较大，则可分x＝m逐条分段统计．

探究提高

线性目标函数的最大(小)值一般在可行域的顶点处取得，也可能在边界处取得．求线性目标函数的最优解，要注意分析线性目标函数所表示的几何意义——在y轴上的截距或其相反数．

探究提高

解线性规划应用问题的一般步骤是：1分析题意，设出未知量；2列出线性约束条件和目标函数；3作出可行域并利用数形结合求解；4作答．

批阅笔记

本题是线性规划的综合应用，考查的是非线性目标函数的最值的求法．解决这类问题的关键是利用数形结合的思想方法，给目标函数赋予一定的几何意义．本题错误率较高．出错原因是，很多学生无从入手，缺乏数形结合的应用意识，不知道从其几何意义入手解题．

方法与技巧

平面区域的画法：二元一次不等式的标准化与半平面的对应性．对于A>0的直线l：Ax＋By＋C＝0，Ax＋By＋C>0对应直线l右侧的平面；Ax＋By＋C<0对应直线l左侧的平面．由一组直线围成的区域形状常见的有：三角形、四边形、多边形以及扇形域和带状域等．转化：求二元一次函数z＝ax＋by (ab≠0)的最值，将函数z＝ax＋by转化为直线的斜截式：y＝－a/bx＋z/b，通过求直线的截距的最值间接求出z的最值．实数最优解一定在顶点或边界取得；经过区域内整数最优解的直线距实数最优解最近．