前阵子出过一道 ( ),有一些网友踊跃提供了自己的思路。在公布我的做法之前,我想先讲讲其中需要利用到的一个有关三角函数的公式以及其证明,大家可以先了解一下三角函数的定义:
先来看看两角和差的三角函数公式的内容吧,真是又对称又神奇吧:
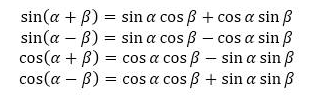
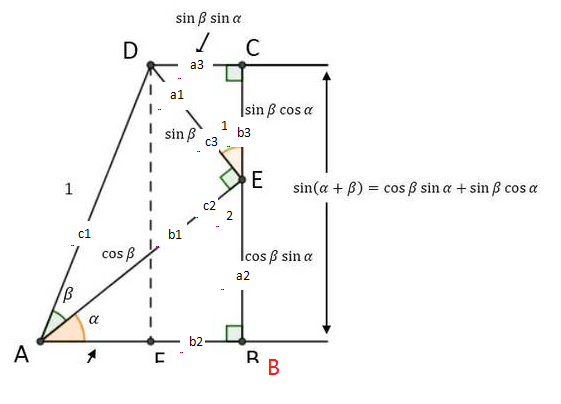
证明方法并不唯一,在这里提供一种我认为比较容易理解的方法。如下图所示,从 A 出发作 ∠α 和 ∠β,在 ∠β 的一条射线上取一点 D ,过 D 作 ∠β 的另一条射线的垂线,设垂足为 E。然后过 E 作∠α 的另一条射线的垂线,设垂足为 B。再延长 EB,作 CD ⊥ CE。
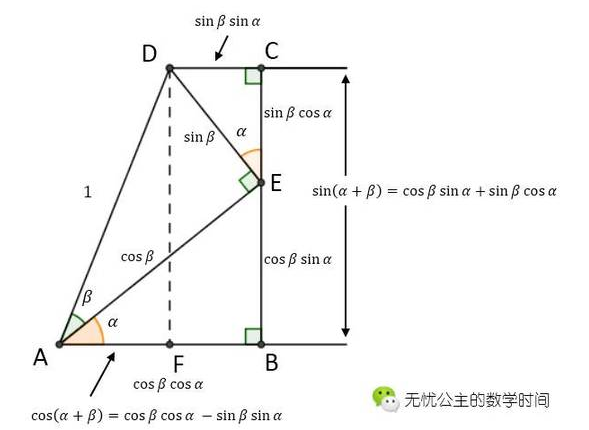
如果假设 AD = 1,那么在 △AED 中,AE = cosβ,DE = sinβ。先来证明第 1 个公式:在 △CDE 中,CE = sinβ cosα;在 △ABE 中,BE = cosβ sinα;在 △ADF 中,DF = sin ( α+β )。因为 DF = BC = BE + CE,所以 sin ( α+β ) = cosβ sinα + sinβ cosα。如果需要证明第 2 个式子,可将 -β 看作一个整体代入第 1 个式子。
然后我们用类似的办法证明第 3 个式子:在 △ABE 中,AB = cosβ cosα;在 △CDE 中,CD = sinβ sinα;在 △AFD 中,AF = cos( α+β ) 。因为 AF = AB - CD,所以 cos ( α+β ) = cos β cosα - sinβ sinα。同理,如果需要证明第 4 个式子,可将 -β 看作一个整体代入第 3 个式子。
不过这个两角和差的三角函数公式有什么用呢?敬请期待 烧脑几何题 142 的解题思路吧!

如上面, 若是cos(-30) 等于 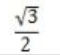 并且 sin(-30) 等于 -0.5 那么
并且 sin(-30) 等于 -0.5 那么
sin30读就可以变为 : sin(60 - 30) = sin60 x cos(-30) + cos(60)X sin(-30)
如何才能实现上述情况?
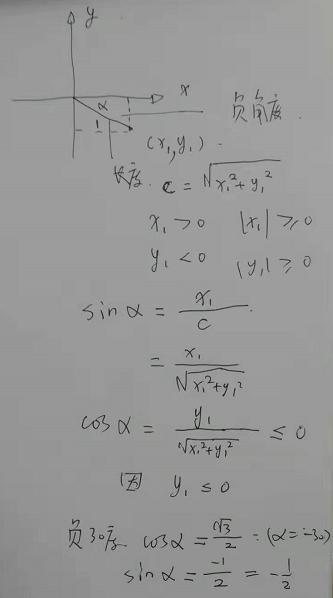
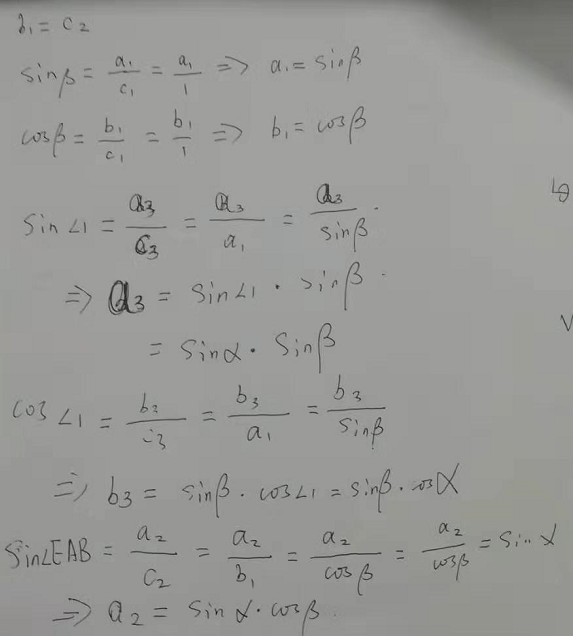
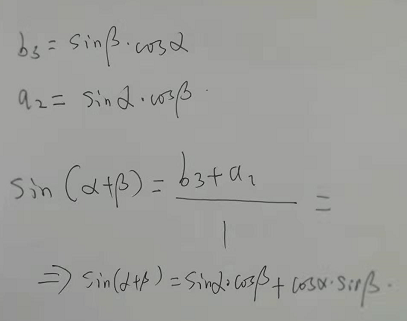
来源: http://m.sohu.com/a/153773930_99893619