问题描述

求任意两个正整数的最大公约数（GCD）。

问题分析

如果有一个自然数a能被自然数b整除，则称a为b的倍数，b为a的约数。几个自然数公有的约数，叫做这几个自然数的公约数。公约数中最大的一个公约数，称为这几个自然数的最大公约数。

根据约数的定义可知，某个数的所有约数必不大于这个数本身，几个自然数的最大公约数必不大于其中任何一个数。要求任意两个正整数的最大公约数即求出一个不大于其中两者中的任何一个，但又能同时整除两个整数的最大自然数。

算法设计

思路有两种：第一种，采用穷举法按从小到大（初值为1，最大值为两个整数当中较小的数）的顺序将所有满足条件的公约数列出，输出其中最大的一个；第二种，按照从大（两个整数中较小的数）到小（到最小的整数1）的顺序求出第一个能同时整除两个整数的自然数，即为所求。

下面对第二种思路进行详细说明。

两个数的最大公约数有可能是其中的小数，所以在按从大到小顺序找寻最大公约数时，循环变量i的初值从小数n开始依次递减，去寻找第一个能同时整除两整数的自然数，并将其输出。需要注意的是，虽然判定条件是i>0，但在找到第一个满足条件的i值后，循环没必要继续下去，如，25和15，最大公约数是5，对于后面的4、3、2、1没必要再去执行，但此时判定条件仍然成立，要结束循环只能借助break语句。

程序流程图：

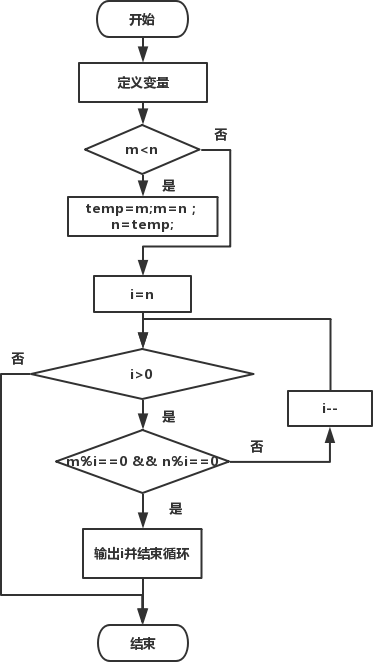
下面是完整的代码：

#include<stdio.h>
int main()
{
int m, n, temp, i;
printf("Input m & n:");
scanf("%d%d", &m, &n);
if(m<n) /*比较大小，使得m中存储大数，n中存储小数*/
{ /*交换m和n的值*/
temp=m;
m=n;
n=temp;
}
for(i=n; i>0; i--) /*按照从大到小的顺序寻找满足条件的自然数*/
if(m%i==0 && n%i==0)
{/*输出满足条件的自然数并结束循环*/
printf("The GCD of %d and %d is: %d\n", m, n, i);
break;
}
return 0;
}

运行结果：
Input m & n:100 125
The GCD of 125 and 100 is: 25

来源： http://c.biancheng.net/view/507.html

--------------------------------

最大公约数

根据最大公约数的如下3条性质，采用递归法编写计算最大公约数的函数Gcd()，在主
函数中调用该函数计算并输出从键盘任意输入的两正整数的最大公约数。
性质1 如果a>b，则a和b与a-b和b的最大公约数相同，即Gcd(a, b) = Gcd(a-b, b)
性质2 如果b>a，则a和b与a和b-a的最大公约数相同，即Gcd(a, b) = Gcd(a, b-a)
性质3 如果a=b，则a和b的最大公约数与a值和b值相同，即Gcd(a, b) = a = b
要求如下：
（1）从键盘任意输入的两整数
主函数调用Gcd()函数，并输出两整数的最大公约数。
（2）Gcd函数原型为：
int Gcd(int a, int b);
如果输入的数不是正整数，则返回-1，否则，返回两个数的最大公约数。
（3）**输入提示信息格式要求："Input a,b:"
输入两个整数时用,号分隔
**输出提示信息要求：
若输入不是正整数，则输出"Input number should be positive!\n"
否则输出"Greatest Common Divisor of %d and %d is %d\n"

#include <stdio.h>
#include <stdlib.h>

int Gcd(int a, int b);

int Gcd(int a, int b)
{
if(a<=0||b<=0)
return -1;
else if(a>b)
return Gcd(a-b, b);
else if(a<b)
return Gcd(a, b-a);
else
return a;
}

int main()
{
int a,b,res;
printf("Input a,b:");
scanf("%d,%d",&a,&b);
res=Gcd(a,b);
if(res==-1)
printf("Input number should be positive!\n");
else
printf("Greatest Common Divisor of %d and %d is %d\n",a,b,res);
return 0;
}

----------------------------

C++最大公约数（递归）详解

使用递归可以计算两个数字的最大公约数。根据欧几里得算法，两个正整数 x 和 y 的最大公约数的计算方法如下:

gcd(x，y) = y; 如果y除以x而没有余数
gcd(x，y) = gcd(y, x/y的余数)；否则

这个定义指出，如果 x/y 没有余数，则 x 和 y 的最大公约数是 y；否则，答案就是 y 和 x/y 的余数的最大公约数。

下面的程序显示了递归的 C++ 实现：

// This program demonstrates a recursive function to
// calculate the greatest common divisor (gcd) of two numbers.
#include <iostream>
using namespace std;
// Function prototype
int gcd(int, int);
int main()
{
int num1, num2;
cout << "Enter two integers: ";
cin >> num1 >> num2;
cout << "The greatest common divisor of " << num1;
cout << " and " << num2 << " is ";
cout << gcd(num1, num2) << endl;
return 0;
}
int gcd(int x, int y)
{
if (x % y == 0) //base case
return y;
else
return gcd{y, x % y);
}

程序输出结果：

Enter two integers: 49 28
The greatest common divisor of 49 and 28 is 7

----------------------------------

用递归求三个数的最大公约数，，，好难啊，，怎么求，，我新手啊，，想了半天
老班的题目啊：声明求最大公约数的递归方法，
写出求两个整数a,b的最小公倍数、三个整数最大公约数的调用语句。
public class GCD_LCM {

public static void main(String[] args) {
int a = 0;
int b = 0;
int c = 0;

a = 1; b = 2; c = 3;
System.out.println(a + " " + b + " " + c + "'s gcd:" + gcd(a, b, c));
System.out.println(a + " " + b + "'s lcm:" + lcm(a, b));

a = 10; b = 20; c = 30;
System.out.println(a + " " + b + " " + c + "'s gcd:" + gcd(a, b, c));
System.out.println(a + " " + b + "'s lcm:" + lcm(a, b));
}

public static int gcd(int a, int b, int c) { // Greatest Common Divisor
return gcd(gcd(a, b), c);
}

public static int gcd(int a, int b) { // Greatest Common Divisor
if (a == 0) {
return b;
} else {
while (b != 0) {
if (a > b) {
a = a - b;
} else {
b = b - a;
}
}
return a;
}
}

public static int lcm(int a, int b) { // Least Common Multiple
return a * b / gcd(a, b);
}
}
输出：
1 2 3's gcd:1
1 2's lcm:2
10 20 30's gcd:10
10 20's lcm:20

------------------------------------

最大公约数的一些定理

定理1：gcd(a,b)能整除所有a,b的公因子。

定理2：若d=gcd(a,b)那么gcd(a/d,b/d)=1。

定理3：gcd(a,b)=gcd(a+cb,b)。

定理4：gcd(a,b)是ax+by中最小的正整数。

推论4.1：若gcd(a,b)=1，那么存在x,y使得ax+by=1。

定理5：gcd(a1,a2,....an)满足交换律和结合律（可以用分治法nlogn求出）。

定理6：如果x,y是实数，那么max(x,y)+min(x,y)=x+y。

定理7：对于有理数x,存在唯一互质的两个数a,b使得x=a/b。

推论7.1：对于无理数x,不存在互质的两个数a,b使得x=a/b。

证明：假设x=sqrt(2)是有理数，那么x=a/b，x2 =a2 /b2 ，2b2 =a2 。