算法–递推策略

资料

递推法是一种重要的数学方法，在数学的各个领域中都有广泛的运用，也是计算机用于数值计算的一个重要算法。这种算法特点是：一个问题的求解需一系列的计算，在已知条件和所求问题之间总存在着某种相互联系的关系，在计算时，如果可以找到前后过程之间的数量关系（即递推式），那么，从问题出发逐步推到已知条件，此种方法叫逆推。无论顺推还是逆推，其关键是要找到递推式。这种处理问题的方法能使复杂运算化为若干步重复的简单运算，充分发挥出计算机擅长于重复处理的特点。

递推算法的首要问题是得到相邻的数据项间的关系（即递推关系）。递推算法避开了求通项公式的麻烦，把一个复杂的问题的求解，分解成了连续的若干步简单运算。一般说来，可以将递推算法看成是一种特殊的迭代算法。

引例：Fibonacci数列

Fibonacci数列的代表问题是由意大利著名数学家Fibonacci于1202年提出的“兔子繁殖问题”(又称“Fibonacci问题”)。

问题：

一个数列的第0项为0，第1项为1，以后每一项都是前两项的和，这个数列就是著名的裴波那契数列，求裴波那契数列的第N项。

算法：

f[0]:=0; f[1]:=1;

for i:=2 to n do f[i]:=f[i–1]+f[i–2];

总结:

从这个问题可以看出，在计算裴波那契数列的每一项目时，都可以由前两项推出。这样，相邻两项之间的变化有一定的规律性，我们可以将这种规律归纳成如下简捷的递推关系式：Fn=g(Fn-1)，这就在数的序列中，建立起后项和前项之间的关系。然后从初始条件（或是最终结果）入手，按递推关系式递推，直至求出最终结果（或初始值）。很多问题就是这样逐步求解的。

对一个试题，我们要是能找到后一项与前一项的关系并清楚其起始条件（或最终结果），问题就可以递推了，接下来便是让计算机一步步了。让高速的计算机从事这种重复运算，真正起到“物尽其用”的效果。

递推概念

给定一个数的序列H0,H1,…,Hn,…若存在整数n0，使当n>n0时,可以用等号(或大于号、小于号)将Hn与其前面的某些项Hi(0<i<n)联系起来，这样的式子就叫做递推关系。
  • 如何建立递推关系
  • 递推关系有何性质
  • 如何求解递推关系

解决递推问题的一般步骤

  • 建立递推关系式
  • 确定边界条件
  • 递推求解

递推的两种形式

顺推法和倒推法

递推的应用分类

  • 一般递推问题
  • 组合计数类问题
  • 一类博弈问题的求解
  • 动态规划问题的递推关系

（一）递推的应用（一般递推问题）

例题2：输出杨辉三角的前N行（HDOJ2032）

Problem Description
还记得中学时候学过的杨辉三角吗？具体的定义这里不再描述，你可以参考以下的图形：
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Input
输入数据包含多个测试实例，每个测试实例的输入只包含一个正整数n（1<=n<=30），表示将要输出的杨辉三角的层数。
Output
对应于每一个输入，请输出相应层数的杨辉三角，每一层的整数之间用一个空格隔开，每一个杨辉三角后面加一个空行。
Sample Input
2 3
Sample Output
1
1 1
1
1 1
1 2 1
代码如下：
#include <iostream>
using namespace std;
int a[31][31];
int main( )
{
    int i,j,n;
    a[0][0]=a[1][0]=a[1][1]=1;
    for(i=2; i<31; i++) {
        for(j=0; j<=i; j++) {
            if(j==0 || i==j) {
                a[i][j]=1;
            } else {
                a[i][j]=a[i-1][j-1]+a[i-1][j];
            }
        }
    }
    while(cin>>n) {
        for(i=0; i<n; i++) {
            for(j=0; j<=i; j++) {
                if(j!=0) cout<<" ";
                cout<<a[i][j];
            }
            cout<<endl;
        }
        cout<<endl;
    } 
    return 0;
}
例题3 : Hanoi塔问题 .

Hanoi塔由n个大小不同的圆盘和三根木柱a,b,c组成。开始时，这n个圆盘由大到小依次套在a柱上，如图1所示。要求把a柱上n个圆盘按下述规则移到c柱上：

(1)一次只能移一个圆盘；

(2)圆盘只能在三个柱上存放；

(3)在移动过程中，不允许大盘压小盘。

问将这n个盘子从a柱移动到c柱上，总计需要移动多少个盘次？

 
分析

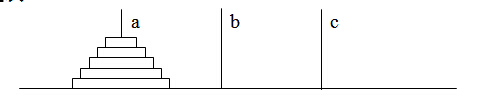
当n=1时：A->C

当n=2时：A->B,A->C,B->C

当n=3时：

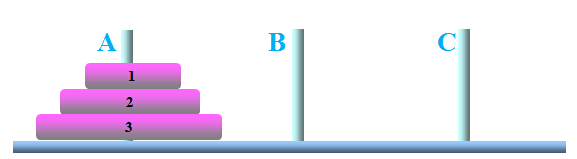
设f(n)为n 个盘子从1柱移到3柱所需移动的最少盘次。

当n=1时，f(1)=1。

当n=2时，f(2)=3。

以此类推，当1柱上有n(n>2)个盘子时，我们可以利用下列步骤：

第一步：先借助3柱把1柱上面的n-1个盘子移动到2柱上，所需的移动次数为f(n-1)。

第二步：然后再把1柱最下面的一个盘子移动到3柱上，只需要1 次盘子。

第三步：再借助1柱把2柱上的n-1个盘子移动到3上，所需的移动次数为f(n-1)。

由以上3步得出总共移动盘子的次数为：f(n-1)+1+ f(n-1)。

所以：f(n)=2f(n-1)+1

hn=2hn-1+1 =2n-1    边界条件：h1=1

（二）递推的应用（组合计数）

例题4：数的计数

【问题描述】我们要求找出具有下列性质数的个数(包含输入的自然数n)，先输入一个自然数n(n≤1000)，然后对此自然数按照如下方法进行处理：
1.不作任何处理；
2.在它的左边加上一个自然数，但该自然数不能超过原数的一半；
3.加上数后，继续按此规则进行处理，直到不能再而 自然数为止；

方法1：用递推

用h[n]表示自然数n所能扩展的数据个数，则：h[1]=1,h[2]=2,h[3]=2,h[4]=4,h[5]=4,h[6]=6,h[7]=6,h[8]=10,h[9]=10。分析上数据，可得递推公式：h[i]=1+h[1]+h[2]+…+h[i/2]。时间复杂度O(n2)。

方法2：是对方法1的改进。我们定义数组s

s(x)=h(1)+h(2)+…+h(x),

h(x)=s(x)-s(x-1)

此算法的时间复杂度可降到O(n)。

方法3：还是用递推

只要做仔细分析，其实我们还可以得到以下的递推公式：

(1)当i为奇数时,h(i)=h(i-1);

(2) 当i为偶数时,h(i)=h(i-1)+h(i/2);

【例题6】传球游戏

【问题描述】上体育课的时候，小蛮的老师经常带着同学们一起做游戏。这次，老师带着同学们一起做传球游戏。
游戏规则是这样的：n（3<=n<=30）个同学站成一个圆圈，其中的一个同学手里拿着一个球，当老师吹哨子时开始传球，每个同学可以把球传给自己左右的两个同学中的一个（左右任意），当老师再吹哨子时，传球停止，此时，拿着球没传出去的那个同学就是败者，要给大家表演一个节目。
聪明的小蛮提出一个有趣的问题：有多少种不同的传球方法可以使得从小蛮手里开始传的球，传了m（3<=m<=30）次后，又回到小蛮手里。两种传球被视作不同的方法，当且仅当这两种方法中，接到球的同学按照顺序组成的序列是不同的。比如3个同学1号、2号、3号，并假设小蛮为1号，球传了3次回到小蛮手里的方式有1->2->3->1和1->3->2->1，共两种。

分析：

设f[i][k]表示经过k次传到编号为i的人手中的方案数，传到i号同学的球只能来自于i的左边一个同学和右边一个同学，这两个同学的编号分别是i-1和i+1，所以可以得到以下的递推公式：

f[i][k]=f[i-1][k-1]+f[i+1][k-1]

f[1][k]=f[n][k-1]+f[2][k-1],   当i=1时

f[n][k]=f[n-1][k-1]+f[1][k-1],   当i=1时

边界条件：f[1][0]=1；结果在f[1][m]中。

核心代码：

cin>>n>>m;
memset(f,0,sizeof(f));
f[1][0]=1;
for(k=1;k<=m;k++)
{   
    f[1][k]=f[2][k-1]+f[n][k-1];
    for(i=2;i<=n-1;i++)f[i][k]=f[i-1][k-1]+f[i+1][k-1];
    f[n][k]=f[n-1][k-1]+f[1][k-1];
}
cout<<f[1][m]<<endl;

（三）递推的应用（组合计数）

Catalan数

定义：Cn=n+2条边的多边形，能被分割成三角形的方案数，例如5边型的分割方案有：

如图，有一个正n+2边形。任取一边，从这边的端点开始，依次顺时针给顶点编号为：0,1,2,3,….,n,n+1(所取的边端点编号为:0,n+1)。这样，除线段所在顶点外，还有n个顶点：1,2,3,…,n。我们以该线段为三角形的一条边，另一个顶点为i(1<=i<=n)。

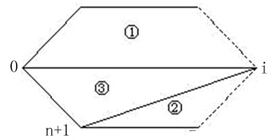
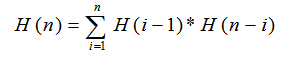
我们设题意要求的三角形剖分方案数为H(n)，即除线段顶点(编号0与n+1)外，还有n个顶点时的三角形剖分方案为H(n)。则以顶点0,i为指定线段(上面还有1,2,…,i-1，共i-1个顶点)的剖分数位H(i-1)；以顶点n+1，i为指定线段的剖分数为H(n-i)。根据乘法原理，以0,i,n+1为一剖分三角形的剖分数应为：H(i-1)*H(n-i)，i=1,2,…,n，所得的剖分各不相同，根据加法原理则有：
这与Catalan数C(n)的表达式是一致的。故本题答案为H(n)=C(n)。

具体实现时，若直接用上述公式计算，对数字的精度要求较高。可将其化为递推式:

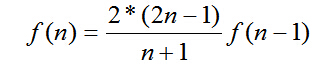
再进行递推计算，并且注意类型的定义要用long long长整型。

（四）递推的应用（博弈问题）

例题：走直线棋问题。

有如下所示的一个编号为1到n的方格：

现由计算机和人进行人机对奕，从1到n，每次可以走k个方格，其中k为集s={a1,a2, a3,....am}中的元素(m<=4)，规定谁最先走到第n格为胜，试设计一个人机对奕方案，摸拟整个游戏过程的情况并力求计算机尽量不败。

分析:

题设条件：若谁先走到第N格谁将获胜，例如，假设S={1,2}，从第N格往前倒推，则走到第N-1格或第N-2格的一方必败，而走到第N-3格者必定获胜，因此在N，S确定后，棋格中每个方格的胜、负或和态（双方都不能到达第N格）都是可以事先确定的。将目标格置为必胜态，由后往前倒推每一格的胜负状态，规定在自己所处的当前格后，若对方无论走到哪儿都必定失败，则当前格为胜态，若走后有任一格为胜格，则当前格为输态，否则为和态。

设1表示必胜态，-1表示必败态，0表示和态或表示无法到达的棋格。

例如，设N＝10，S＝{1,2}，则可确定其每个棋格的状态如下所示：

而N＝10，S＝{2,3}时，其每格的状态将会如下所示：

有了棋格的状态图后，程序应能判断让谁先走，计算机选择必胜策略或双方和（双方均不能到达目标格）的策略下棋，就能保证计算机尽可能不败。

（五）递推的应用（动态规划中的递推）

例题：方格取数

在一个n×m的方格中，m为奇数，放置有n×m个数 ，如图,方格中间的下方有一人，此人可按照五个方向前进但不能越出方格,见右下图。人每走过一个方格必须取此方格中的数。要求找到一条从底到顶的路径，使其数相加之和为最大。输出和的最大值。

分析:

我们用坐标(x,y)唯一确定一个点，其中(m,n)表示图的右上角，而人的出发点是，受人前进方向的限制，能直接到达点(x,y)的点只有(x+2,y-1)，(x+1,y-1)，(x,y-1)，(x-1,y-1)，(x-2,y-1)。到点(x,y)的路径中和最大的路径必然要从(m/2,0)到(x+2,y-1)，(x+1,y-1)，(x,y-1)，(x-1,y-1)，(x-2,y-1)的几条路径中产生，既然要求最优方案，当然要挑一条和最大的路径，关系式如下：

Fx,y= Max{Fx+2,y-1 ,Fx+1,y-1,Fx,y-1,Fx-1,y-1,Fx-2,y-1}+Numx,y，

其中Numx,y 表示(x,y) 点上的数字。

边界条件为：

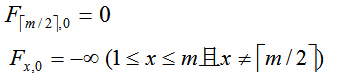
动态规划与递推的关系

上题实质上是采用动态规划来求解,那么与递推动态规划之间到底是什么关系呢？

我们不妨画个图(如下图)。而通常人们理解的递推关系就是一般递推关系，故认为动态规划与递推关系是两个各自独立的个体。

 

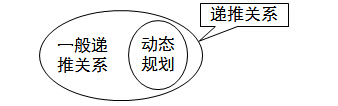
1、一般递推边界条件很明显,动态规划边界条件比较隐蔽,容易被忽视

2、一般递推数学性较强,动态规划数学性相对较弱

3、一般递推一般不划分阶段,动态规划一般有较为明显的阶段

 

PS：更多递推练习，可以看看《递推求解专题练习》

作者：wuyudong
本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利.
如果觉得本文对您有帮助，可以对作者进行小额【赞助】
分类: 算法

 本文地址：http://www.cnblogs.com/archimedes/p/4265019.html，转载请注明源地址。

 

在Hdu上是下面几题：

Hdu 2041 超级楼梯

下面是解题报告（因为有的题有点水，和贴发）

Hdu 2044 一只小蜜蜂...

分析：数一下前几种可能的走法，不难发现这是个斐波那契数。但是题目给定任意两个数a和b（a<b），计算a到b的走法。因为是从a到b的走法，所以从1到a的走法我们不用讨论，同理从1到b的走法我们也不用讨论。这样，就可以将a看做1，将b看做（b-a+1），转化为求从1到（b-a+1）的走法。

o(╯□╰)o：只知道是斐波那契数，但是布吉岛斐波那契数数的增长很快，很容易爆int。

下面是代码：

/*Hdu 2044 一只小蜜蜂...
递推 斐波那契数
数组开long long，斐波那契数增长很快
*/
#include<iostream>
using namespace std;
const int maxn = 60;
long long f[maxn];
int t,a,b;
int main()
{
f[1] = 1;
f[2] = 1;
for(int i = 3; i <= maxn; i++) f[i] = f[i-1] + f[i-2];
cin>>t;
while(t--)
{
cin>>a>>b;
cout<<f[b-a+1]<<endl;
}
return 0;
}

Hdu 2045 不容易系列之(3)—— LELE的RPG难题

分析：

 

下面是代码：
#include<iostream>
using namespace std;
const int maxn = 55;
long long F[maxn];
int n;
int main()
{
F[1] = 3;
F[2] = 6;
F[3] = 6;
for(int i = 4; i <= maxn; i++) F[i] = F[i-1] + 2 * F[i-2];
while(cin>>n) cout<<F[n]<<endl;
return 0;
}

Hdu 2046 骨牌铺方路

分析：前一排只有一种方法，所以只用讨论F[n-1]；前二排也只有一种方法，那么讨论F[n-2]。所以递推式：F[n] = F[n-1] + F[n-2]。这也是斐波那契数。

下面是代码：

#include<iostream>
using namespace std;
const int maxn = 55;
long long f[maxn];
int n;
int main()
{
f[0] = 1;
f[1] = 1;
for(int i = 2; i <= maxn; i++) f[i] = f[i-1] + f[i-2];
while(cin>>n) cout<<f[n]<<endl;
return 0;
}

Hdu 2047 阿牛的EOF牛肉串
分析：设F[n]可以由两个部分得到，第（n-1）个为O，第（n-1）个为O。

F[n] = 2 * (为O) + 3 *（不为O）

下面是代码：

#include<iostream>
using namespace std;
const int maxn = 45;
long long A[maxn];
long long B[maxn];
int n;
int main()
{
A[1] = 1;
B[1] = 2;
for(int i = 2; i <= maxn; i++)
{
A[i] = B[i-1];
B[i] = 2 * (A[i-1] +B[i-1]);
}
while(cin>>n) cout<<A[n]+B[n]<<endl;
return 0;
}
Hdu 2048 神，上帝和老天爷

分析：全错位排列。当n小于8时，用递推求解；当n大于8时，基本上概率不变。不过犯二了，记错变形后的递推公式了，囧！

下面是代码“：

/*Hdu 2048 神，上帝和老天爷
全错位排列
*/
#include<cstdio>
#include<cmath>
using namespace std;
const int maxn = 50;
double D[maxn];
int n;
int main()
{
D[1] = 0;
D[2] = 1;
int t;
scanf("%d",&t);
while(t--)
{
double f = 1;
scanf("%d",&n);
if(n <= 10)
{
for(int i = 2; i <= n; i++)
{
f = f * i;
double flag;
if(i%2 == 0) flag = +1;
else flag = -1;
D[i] = i * D[i-1] + flag;
}
int ans = floor((D[n]/f+0.00005)*10000);
printf("%.2lf%\n",(double)ans/100);
}
else
printf("36.79%10\n");
}
return 0;
}

Hdu 2049 不容易系列之(4)——考新郎

分析：这到题和上一题相似，都是错位排列。只不过上一题是全错位排列，只一题是部分错位排列。但是原理没有什么不一样的。

下面是代码：

#include<iostream>
using namespace std;
const int maxn = 25;
long long F[maxn],C[maxn];
int t,n,m;
int main()
{
F[1] = 0;
F[2] = 1;
C[0] = 1;
for(int i = 3; i <= maxn; i++) F[i] = (i-1) * (F[i-1] + F[i-2]);

cin>>t;
while(t--)
{
cin>>n>>m;
for(int i = 1; i <= n; i++) C[i] = C[i-1]*(n-i+1)/i;
cout<<C[m]*F[m]<<endl;
}
return 0;
}

Hdu 2050 折线分割平面
分析：首先搞清楚直线分割平面问题，然后再根据直线问题解决折线问题。

下面是代码：

#include<iostream>
using namespace std;
int n,t;
int main()
{
cin>>t;
while(t--)
{
cin>>n;
cout<<1 + (2*n)*(2*n+1)/2 - 2*n<<endl;
}
return 0;
}
Hdu 2041 超级楼梯

很简单的递推题，直接代码

#include<iostream>
using namespace std;
const int maxn = 50;
int d[maxn];
int t,n;
void print()
{
d[1] = 1;
d[2] = 1;
for(int i = 3; i < maxn; i++)
{
d[i] = d[i-1] + d[i-2];
}
}
int main()
{
cin>>t;
print();
while(t--)
{
cin>>n;
cout<<d[n]<<endl;
}
return 0;
}

 

好了，前前后后花了不少时间才刷完这几道递推入门题。都是很基础的一些问题。

------------

递推求解专题练习

摘要： hdoj2044--一只小蜜蜂... Problem Description 有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房，不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。 其中，蜂房的结构如下所示。

hdoj2044--一只小蜜蜂...

Problem Description
有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房，不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。
其中，蜂房的结构如下所示。
Input
输入数据的第一行是一个整数N,表示测试实例的个数，然后是N 行数据，每行包含两个整数a和b(0<a<b<50)。
Output
对于每个测试实例，请输出蜜蜂从蜂房a爬到蜂房b的可能路线数，每个实例的输出占一行。
Sample Input
2
1 2
3 6
Sample Output
1
3

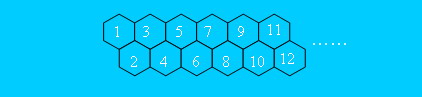
#include <stdio.h>

int main(void)
{
    int i, j, n;
    __int64 d[51] = {1, 1, 2,};

    for (i = 3; i < 51; i++)
        d[i] = d[i-1] + d[i-2];
    scanf("%d", &n);
    while (n-- && scanf("%d%d", &i, &j) != EOF)
        printf("%I64d\n", i > j ? 0 : d[j-i]);

    return 0;
}

 

hdoj2045--不容易系列之(3)—— LELE的RPG难题

Problem Description
人称“AC女之杀手”的超级偶像LELE最近忽然玩起了深沉，这可急坏了众多“Cole”（LELE的粉丝,即"可乐"）,经过多方打探，某资深Cole终于知道了原因，原来，LELE最近研究起了著名的RPG难题:
有排成一行的ｎ个方格，用红(Red)、粉(Pink)、绿(Green)三色涂每个格子，每格涂一色，要求任何相邻的方格不能同色，且首尾两格也不同色．求全部的满足要求的涂法.
以上就是著名的RPG难题.
如果你是Cole,我想你一定会想尽办法帮助LELE解决这个问题的;如果不是,看在众多漂亮的痛不欲生的Cole女的面子上,你也不会袖手旁观吧?
Input
输入数据包含多个测试实例,每个测试实例占一行,由一个整数N组成，(0<n<=50)。
Output
对于每个测试实例，请输出全部的满足要求的涂法，每个实例的输出占一行。
Sample Input
1
2
Sample Output
3
6

#include<stdio.h>

int main()
{
    int i,n;
    double a[51]={0,3,6,6};
    while(scanf("%d",&n)!=EOF)
    {
        for(i=4;i<51;i++)
            a[i]=a[i-2]*2+a[i-1];
        printf("%.lf\n",a[n]);
    }
    return 0;
}

 

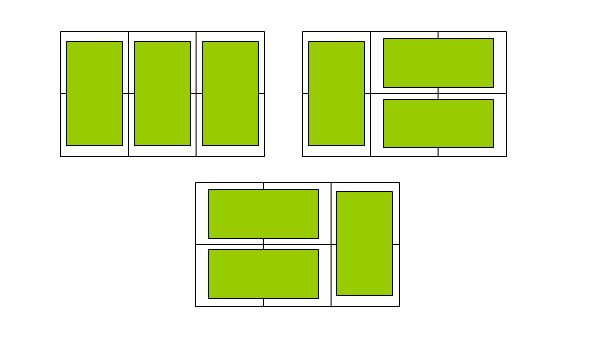
hdoj2046--骨牌铺方格

Problem Description
在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数.
例如n=3时,为2× 3方格，骨牌的铺放方案有三种,如下图：
Input
输入数据由多行组成，每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0<n<=50)。
Output
对于每个测试实例，请输出铺放方案的总数，每个实例的输出占一行。
Sample Input
1
3
2
Sample Output
1
3
2

#include<stdio.h>

int main()
{
    int i,n;
    double a[51]={0,1,2,3};
    for(i=4;i<51;i++)
        a[i]=a[i-2]+a[i-1];
    while(scanf("%d",&n)!=EOF)
    {
        printf("%.lf\n",a[n]);
    }
    return 0;
}

 

hdoj2047--阿牛的EOF牛肉串

Problem Description
今年的ACM暑期集训队一共有18人，分为6支队伍。其中有一个叫做EOF的队伍，由04级的阿 牛、XC以及05级的COY组成。在共同的集训生活中，大家建立了深厚的友谊，阿牛准备做点什么来纪念这段激情燃烧的岁月，想了一想，阿牛从家里拿来了一 块上等的牛肉干，准备在上面刻下一个长度为n的只由"E" "O" "F"三种字符组成的字符串（可以只有其中一种或两种字符，但绝对不能有其他字符）,阿牛同时禁止在串中出现O相邻的情况，他认为，"OO"看起来就像发 怒的眼睛，效果不好。
你，NEW ACMer,EOF的崇拜者，能帮阿牛算一下一共有多少种满足要求的不同的字符串吗？
PS: 阿牛还有一个小秘密，就是准备把这个刻有 EOF的牛肉干，作为神秘礼物献给杭电五十周年校庆，可以想象，当校长接过这块牛肉干的时候该有多高兴！这里，请允许我代表杭电的ACMer向阿牛表示感谢！
再次感谢！
Input
输入数据包含多个测试实例,每个测试实例占一行,由一个整数n组成，(0<n<40)。
Output
对于每个测试实例，请输出全部的满足要求的涂法，每个实例的输出占一行。
Sample Input
1
2
Sample Output
3
8

#include<stdio.h>

int main()
{
    int i,n;
    __int64 a[41]={0,3,8};
    for(i=3;i<41;i++)
        a[i]=(a[i-2]+a[i-1])*2;
    while(scanf("%d",&n)!=EOF)
    {
        printf("%I64d\n",a[n]);
    }
    return 0;
}

 

hdoj2048--神、上帝以及老天爷

Problem Description
HDU 2006'10 ACM contest的颁奖晚会隆重开始了！
为了活跃气氛，组织者举行了一个别开生面、奖品丰厚的抽奖活动，这个活动的具体要求是这样的：
首先，所有参加晚会的人员都将一张写有自己名字的字条放入抽奖箱中；
然后，待所有字条加入完毕，每人从箱中取一个字条；
最后，如果取得的字条上写的就是自己的名字，那么“恭喜你，中奖了！”
大家可以想象一下当时的气氛之热烈，毕竟中奖者的奖品是大家梦寐以求的Twins签名照呀！不过，正如所有试图设计的喜剧往往以悲剧结尾，这次抽奖活动最后竟然没有一个人中奖！
我的神、上帝以及老天爷呀，怎么会这样呢？
不过，先不要激动，现在问题来了，你能计算一下发生这种情况的概率吗？
Input
输入数据的第一行是一个整数C,表示测试实例的个数，然后是C 行数据，每行包含一个整数n(1<n<=20),表示参加抽奖的人数。
Output
对于每个测试实例，请输出发生这种情况的百分比，每个实例的输出占一行, 结果保留两位小数(四舍五入)，具体格式请参照sample output。
Sample Input
1
2
Sample Output
50.00%

错排：n封信放入n个信封，要求全部放错，共有多少种放法，记n个元素的错排总数为f(n)

假设有n封信，第一封信可放在(2-n)的任一个信封里，共n-1种放法，设第一封信放在了第k个信封里，若此时第k封信放在了第1个 信封里，则只要将剩下的n-2错排，即f(n-2)，若第k封信没有放在了第1个信封里，可将第1封信的位置看成是“第k个位置”，即将n-1封信错排， 即为f(n-1)

由递推可得：f(n)=(n-1)*(f(n-1)+f(n-2))

#include<stdio.h>

int main()
{
    int C,n;
    int i;
    double a[21]={0,0,1};
    for(i=3; i<21; i++)
    {
        a[i]=(i-1)*(a[i-2]+a[i-1]);
    }
    while(scanf("%d",&C)!=EOF)
    {
        while(C--)
        {
            scanf("%d",&n);
            a[n]*=1.0;
            for(i=2; i<=n; i++)
                a[n]/=i;
            printf("%.2lf%%\n",a[n]*100);

        }
    }
    return 0;
}

 

算法设计与分析——第三篇，倒推蛮力什么的

写在前面的话——

这次主要是就是开始讲算法了，主要的来说，主要是分治法、贪婪法还有动态规划，这些我觉得是一种处理问题的思想，还有什么蛮力法，倒推法什么的，也算是思想，但是更多的，这个也算是一种工具，会比较常见的用在之前的三种方法中，特别是倒推，其实我也觉得倒推并没有多神奇，毕竟我们做数学题的时候，就是很多时候按照正常的顺序思考不出来，反着推就能比较顺利，而且我觉得这些个算法，只能算是训练，而实际应用的时候，应该还是适可而止，不要过分强求，实际问题一般都比这些训练题复杂得多，所以我始终觉得这个只是锻炼一个思想而已！

第二篇——

我觉得下面三个题比较简单，就是第一个题有点难度，不过因为是书上例题，所以并没有花很多功夫去思考，反过来想的话，这个题也没法想的太细，因为需要很多数学思想的支撑，特别是一开始要建立一个数学模型，所以掌握方法领悟技巧就好，至于为什么要这么算，凭什么这么算就是最节约的，不讨论比较好。

1.穿越沙漠问题

一辆吉普车穿越1000千米的沙漠。吉普车的总装油量为500加仑，耗油量为1加仑/千米。由于沙漠中没有油库，必须先用这辆车在沙漠中建立临时油库。若吉普车用最少的耗油量穿越沙漠，应在那些地方建立油库，以及各处存储的油量。

 

算法设计：

这个题由于要求用最少的耗油量，也就是最后穿越沙漠之后刚好油量为0，同时，很明显，直接开是无法穿越的，在中间架设油库，只能使用这辆车，一次最所携带500加仑并且行进返回都需要耗油，如果正向分析问题会非常复杂无从下手，但是倒推会发现还是有迹可寻。

从终点倒推，刚好油量为0，则在离终点500千米的地方A建立一个油库并且存油500加仑，设A点之后的油库在B点，从B点到A点运油，满足条件的最佳方案是B点到A点共走三次，第一、二次来回耗油量为装载量的2/3，储油量为装载量的1/3，第三次单向行驶耗油量为装载量的1/3，储油量为装载量的2/3。统计一下，B点的储油量为1000加仑，此段长度为500/3千米。

同理分析B点之后的油库C点，应该需要往返5次，位置就在距离B点500/5千米的位置，存油量为1500，以此类推

 

代码如下：

  1. #include <stdio.h>
  3. int main()
  4. {
  5. int dis[100],k,oil[100];
  6. dis[1]= 500;
  7. k= 1;
  8. oil[1]= 500;
  9. do {
  10. k++;
  11. dis[k]= dis[k-1] + 500/(2 * k - 1);
  12. oil[k]= 500 * k;
  13. }while(dis[k] < 1000);
  15. oil[k]= 500 * (k - 1) + (1000 - dis[k]) * (2 * k - 1);
  16. dis[k]= 1000;
  18. int i = 0;
  19. for(;i<k;i++) {
  20. printf("第%d个临时油库在距离起点%d的位置，储油量为%d\n",i+1,1000-dis[k-i],oil[k-i]);
  21. }
  23. return 0;
  24. }

算法分析：通过倒推法可以解决一些正向推导很难处理的问题，非常有效。

 

2.54张扑克牌，两个人轮流拿牌，每个人每次最少取1张，最多取4张，谁拿最后一张谁输。编写模拟计算机先拿牌且必胜的算法。

 

算法设计：

根据题意，必须先拿且必胜，则可以理解为，在54张减去第一次拿的牌数后，每轮对方先拿，自己后拿，直到最后一轮，刚好剩下1张牌，且对方的拿牌数为一个1-4的随机数，那么此时应该考虑，对方每次的拿牌数是不能确定的，但是每轮的拿牌数是可以确定的，就是可以在对方拿完之后，自己拿一定数量的牌凑成一个可以一定达成的数字，这个数字很明显应该是5，即每轮拿5张牌，最后还剩一张，且之前减去了已经拿走的牌，则很明显，先拿走3张之后，还剩51张，每轮拿走5张，十轮之后，还剩一张，此时必定获胜。

 

代码如下：

  1. #include <stdio.h>
  2. #include <stdlib.h>
  3. #include <time.h>
  5. int main()
  6. {
  7. int i = 3;//计算机初始拿的牌数
  8. int n = 54;//当先的牌数量
  9. int i_times = 1;//总计拿了多少次
  10. int p;//另一方的拿牌数，在1-4之间随机生成一个数
  11. srand(time(0));
  12. while(n > 0)
  13. {
  14. p= rand()%4 + 1;
  15. printf("the%d time computer select %d paper and you %d paper\n",i_times,i,p);
  16. n-= i+p;
  17. printf("nowthe paper has left %d\n",n);
  18. i_times++;
  19. i= 5 - p;//需要在对方拿牌之后，再取的牌数和之前的牌数凑成固定的5张
  20. if(n - i == 1) {//如果还剩一张，此时不可以继续随机了，只能拿这张牌
  21. printf("the%d time computer select %d paper and you have the last one\n",i_times,i);
  22. break;
  23. }
  24. }
  25. return 0;
  26. }

算法分析：这个算法的关键在于如何保证最后一定剩一张牌给另一方，而且要保证每一轮拿牌保证一样的数量才可以进行控制，但是每一轮先拿牌的话，就无法控制，只能再对方先拿牌之后才能根据他的数量再决定该拿多少张，此时根据规则，必须先拿又必须赢，此时需要考虑先拿多少张，然后开始每一轮拿牌，最后剩一张牌，顺利写出代码

 

 

3.有一堆棋子，2枚2枚的数，最后余1枚；3枚3枚的数，最后余2枚；5枚5枚的数，最后余4枚；6枚6枚的数，最后余5枚；7枚7枚的数，最后正好数完。变成求出这堆棋子最少有多少枚棋子。

 

算法设计：

从题目来看，很明显是求一个数，这个数对2求余得1，对3求余得2，对5求余得4，对6求余得5，对7整除，使用蛮力法，从最小的数7开始累加，直到满足条件结束

 

代码如下：

  1. int main()
  2. {
  4. int i = 7;
  5. while(1) {
  6. if(5 == i % 6 && 4 == i% 5 && 2 == i % 3 &&1 == i % 2) {
  7. printf("这堆棋子的数量为%d\n",i);
  8. break;
  9. }else
  10. i+= 7;
  11. }
  13. return 0;
  14. }

算法分析：以上实际采用枚举法，将每一个数都进行运算求得余数进行比对，直到符合所有条件的数出现为止，这里简单设计了下，不用每个数都判断，只需要判断7的倍数即可，可以减少循环次数，整个算法看起来比较清晰简洁。

 

----------------------

穷举算法和递推算法（Java）

穷举算法

概念：

最简单算法，依赖计算机的强大计算能力穷尽每一种可能的情况。穷举算法效率不高，但是适合一些没有明显规律可循的场合。

 

思想：

在使用穷举算法时，需要明确问题答案的范围，这样才可能在指定范围搜索答案。指定范围之后，就可以使用循环和条件判断语句进行逐步验证结果了。

 

案例：鸡兔同笼问题

在一个笼子里关着若干只鸡和若干兔子。一共有35个头，和94只脚。问在一个笼子里鸡和兔子各有多少个。

复制代码
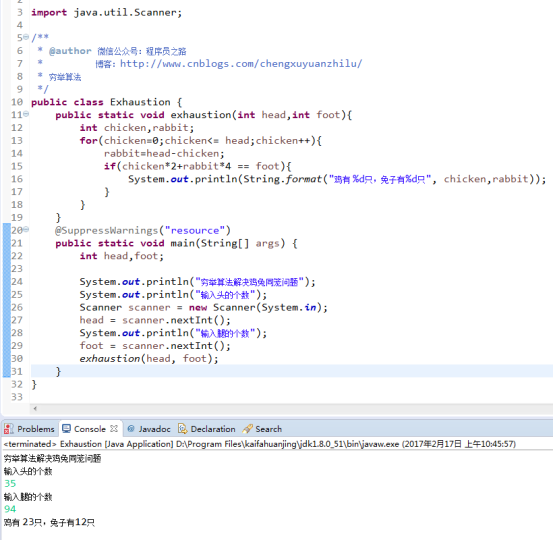
package cmd.chengxuyuanzhilu.arithmetic;

import java.util.Scanner;

/**
 * @author 微信公众号：程序员之路 
 *                 博客：http://www.cnblogs.com/chengxuyuanzhilu/
 * 穷举算法
 */
public class Exhaustion {
    public static void exhaustion(int head,int foot){
        int chicken,rabbit;
        for(chicken=0;chicken<= head;chicken++){
            rabbit=head-chicken;
            if(chicken*2+rabbit*4 == foot){
                System.out.println(String.format("鸡有 %d只，兔子有%d只", chicken,rabbit));
            }
        }
    }
    @SuppressWarnings("resource")
    public static void main(String[] args) {
        int head,foot;
        
        System.out.println("穷举算法解决鸡兔同笼问题");
        System.out.println("输入头的个数");
        Scanner scanner = new Scanner(System.in);
        head = scanner.nextInt();
        System.out.println("输入腿的个数");
        foot = scanner.nextInt();
        exhaustion(head, foot);
    }
}
复制代码

 

递推算法

概念：

递推算法在数学计算等方面广泛应用。递推算法适合有着明显规律的场合

 

思想：

递推算法往往需要用户知道答案和问题之间的逻辑关系。在许多数学问题中，都有着明显的计算公式可以遵循，因此可以采用递推算法。

 

案例：兔子产崽子的问题

如果有两个月大的兔子以后每个月都可以产一对小兔子，而一对小兔子出生两个月后可以在生小兔子，也就是1月份出生，3月份才可以产崽子。那么假定一年内没有发生死亡事件，那么现在有一对小兔子一年后共有多少对兔子。

 

案例分析：

1月 1对兔子

2月 1对兔子

3月 2对兔子 一对成熟兔子

4月 3对兔子

5月 5对兔子 两对成熟兔子

6月 8对兔子 三对成熟兔子

。。。。。。

规律：前两个月都是一对兔子，以后每个月的兔子的对数是前两个月的总和

除1,2月份的计算公式：n月  Fn = (Fn-1)+(Fn-2)

复制代码
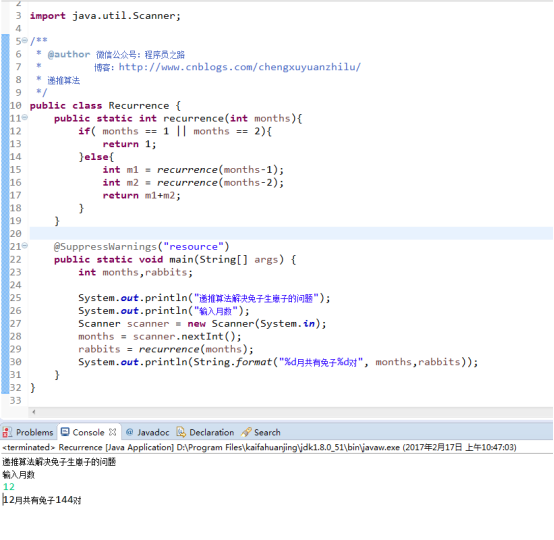
package cmd.chengxuyuanzhilu.arithmetic;

import java.util.Scanner;

/**
 * @author 微信公众号：程序员之路 
 *                 博客：http://www.cnblogs.com/chengxuyuanzhilu/
 * 递推算法
 */
public class Recurrence {
    public static int recurrence(int months){
        if( months == 1 || months == 2){
            return 1;
        }else{
            int m1 = recurrence(months-1);
            int m2 = recurrence(months-2);
            return m1+m2;
        }
    }
    
    @SuppressWarnings("resource")
    public static void main(String[] args) {
        int months,rabbits;
        
        System.out.println("递推算法解决兔子生崽子的问题");
        System.out.println("输入月数");
        Scanner scanner = new Scanner(System.in);
        months = scanner.nextInt();
        rabbits = recurrence(months);
        System.out.println(String.format("%d月共有兔子%d对", months,rabbits));
    }
}