弧度是怎么来的？为何要用弧度？起源是什么？

角度

谈弧度，就必须先谈下角度，如果世界上只有弧度，没有角度，我相信大家也就不会疑惑为什么会有弧度制了。

角度为什么出现？

角度的出现，是源于对圆周运动的观察。

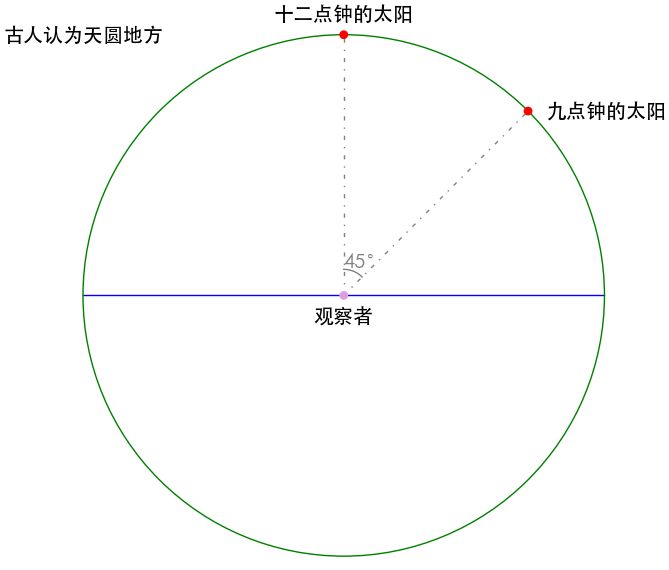
这个世界上最大最显眼的圆周运动就是太阳，就算我们现代人知道地心说是错误的，可是以我们的尺度来说，抬头还是观察到太阳在做圆周运动。

作为观察者，我们也非常自然的，以我们为中心，开始计算太阳相对我们的移动，这就开始出现了角度。

圆周为什么是360°？

地球围绕太阳公转，而遥远的十二星座仿佛固定在圆柱形天幕上:

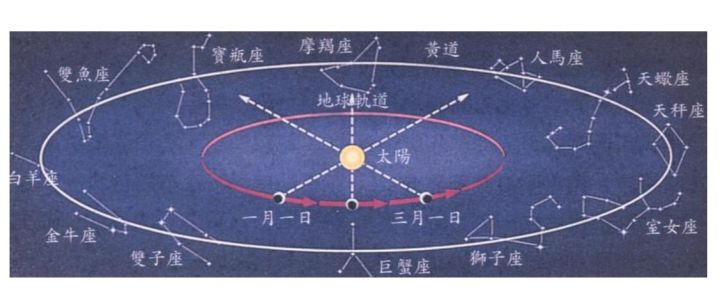
地球上的我们就像看走马灯一样，随着地球的公转，在特定的时间看到特定的星座。古人发现了这个规律，并且以星座为参照物，近似观察出循环周期为360天，也就是一年。

因此，天就被等分成了360份，也就是圆被等分成了360份。虽然后来古人慢慢发现了一年实际上是365天，但是因为360度已经成为习惯，并且非常好计算，所以就被保留了下来。

度数是圆周的占比

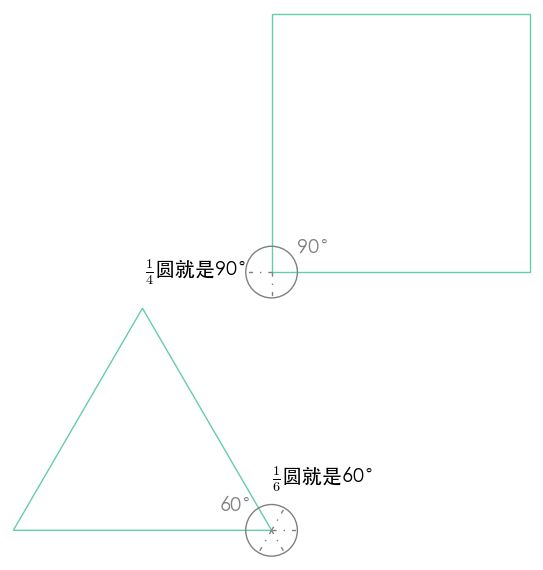
弧度

角度似乎已经足够描述圆周运动了，为什么要出现弧度？是来给世界添乱的吗？

弧度为什么出现？

弧度的出现，刚开始不过是个数学游戏。弧度＝弧长/半径，对于相同的角度这个比值保持不变，所以可以看作角度的另一种表现形式。(其实“弦长/半径”也是定值，为啥不选这个作为弧度呢？可以想想。)

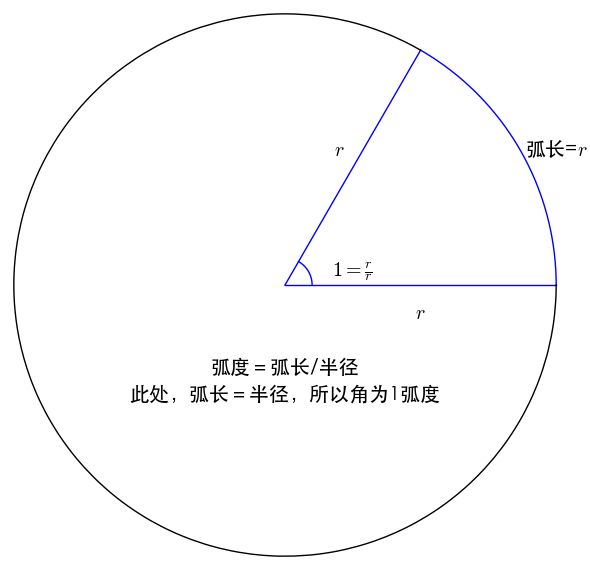
弧度有什么现实意义？

弧度是从圆周运动进行者的角度来看待圆周运动。

之前说过，古人的世界观是天圆地方，人们的旅行都被视为直线运动。欧式几何里面的直线笔直的延伸到无穷远处。

可是，事实是，地球是圆的，随着技术的发展，大航海时代的来临，大家越来越认识到这一点。传统意义上的直线，在地球表面都不复存在，必须重新定义直线的含义。

弧度也是在这样的环境下开始发扬光大：

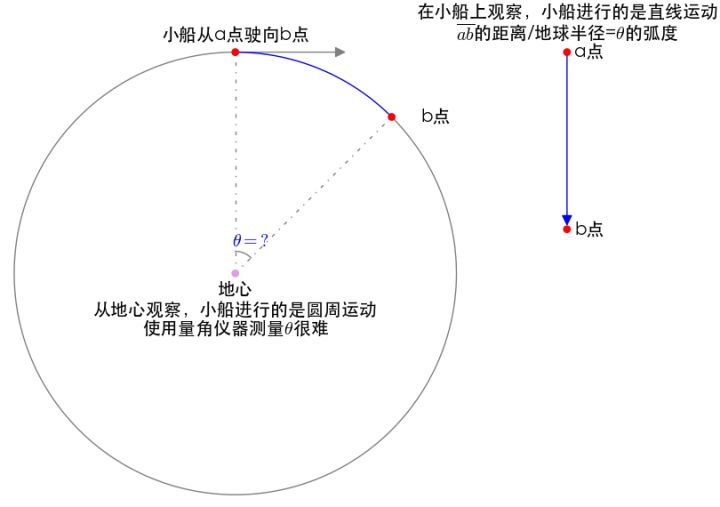
知道了移动的角度，也就知道了经纬度，就可以通过地图进行导航，而利用弧度，大大简化了这一过程。

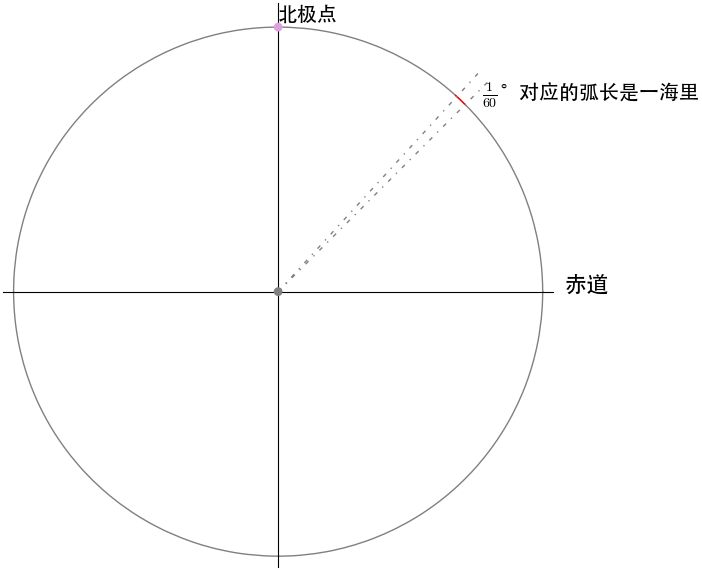
“海里”这个航海单位也是弧度在大航海时代的产物。

“海里”传统上定义为子午线1角分的长度。它可从航海图中，以子午线上的纬度的改变来量度。----维基百科

弧度可以把圆周运动转为直线运动

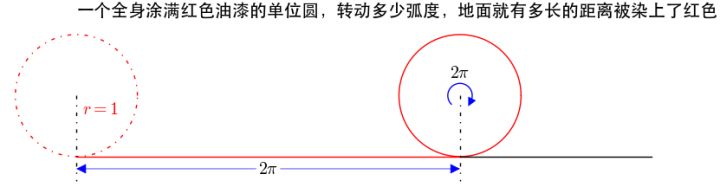
这种转换有了之后，就可以很方便的测量汽车的直线速度了。汽车在车胎附近安装一个传感器，测出车胎的转速（比如10弧度/秒），乘以半径（比如1米），就得到了汽车的直线速度（这里就是10米/秒)。有的出租车换了更小直径的轮胎而不修改行车电脑里面的轮胎半径，就可以轻松的“偷里程”。所以，学习多么的重要啊！

弧度帮助理解重要极限

$\displaystyle {\lim _{x \to 0}\frac{sin(x)}{x}}=1$ ，这是个很重要的极限，考试也会经常用到，但是他的几何意义是什么呢？

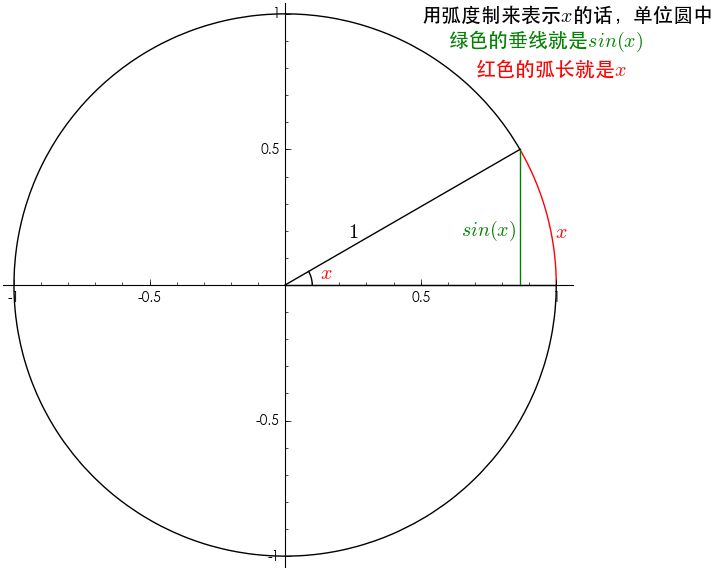
在现代数学中，弧度是最基本的概念

弧度使得角度和实数统一在了一起。对于 $f(x)=sin(x)$ 这个函数而言，如果 $x$ 使用角度，就很难去理解这个方程，一边的单位是度，一边是无单位的实数。而使用弧度可以很好的解决这一问题，使得 $x$ 和 $y$ 都是无单位的数。

弧度开启了三角函数的大门。欧拉在他的著作《无穷小分析概论》就提出了弧度，并且作出了三角函数线（这也是非常有趣的概念，在这里就不展开了），通过弧度和三角函数线，第一次定义了三角函数！这也是欧拉在数学上的重大贡献之一。此时，三角分析才开始和函数这个有力的工具挂上钩。

结论

角度是对圆周运动的观察，弧度是对圆周运动的进行
角度是有单位的，弧度是无单位的，所有三角函数都应使用弧度

个人觉得，在现代教育中，弧度制应该尽早的引入，而去弱化角度制，让学生尽早形成对弧度制的直觉认知。就好比加减乘除虽然重要，但是在微积分才是现代数学的基础。

来源： https://www.zhihu.com/question/40759023

--------------------

弧度制的历史简介

一、弧度制的发明——托勒密

克劳迪亚斯托勒密大约于公元90年出生在希腊。托勒密同斯特雷波一道为地理学和绘制学的研究奠定了基础。托勒密在天文学、光学和音乐方面也颇有造诣。真正创立了天文学，并且计算出诸多天体运行轨迹的是两千年前古罗马时代的托勒密。虽然今天我们可能会嘲笑托勒密犯的简单的错误，但是真正了解托勒密贡献的人都会对他肃然起敬。托勒密发明了球坐标，定义了包括赤道和零度经线在内的经纬线，他提出了黄道，还发明了弧度制。

当然，他最大也是最有争议的发明是地心说。虽然我们知道地球是围绕太阳运动的，但是在当时，从人们的观测出发，很容易得到地球是宇宙中心的结论。从地球上看，行星的运动轨迹是不规则的，托勒密的伟大之处是用四十个小圆套大圆的方法，精确地计算出了所有行星运动的轨迹。（托勒密继承了毕达格拉斯的一些思想，他也认为圆是最完美的几何图形。）托勒密模型的精度之高，让以后所有的科学家惊叹不已。即使今天，我们在计算机的帮助下，也很难解出四十个套在一起的圆的方程。每每想到这里，我都由衷地佩服托勒密。一千五百年来，人们根据他的计算决定农时。但是，经过了一千五百年，托勒密对太阳运动的累积误差，还是差出了一星期。

二、弧度制思想的提出——欧拉

18世纪以前，人们一直是用线段的长来定义三角函数的．瑞士数学家欧拉(Leonhardo Eulero，1707年～1783年)在他于1748年出版的一部划时代的著作《无穷小分析概论》中，提出三角函数是对应的三角函数线与圆半径的比值，并令圆的半径为1，使得对三角函数的研究大为简化．这是欧拉在数学史上的重要功绩之一．

其次，欧拉在上述著作的第八章中提出了弧度制的思想．他认为，如果把半径作为1个单位长度，那么半圆的长就是π，所对圆心角的正弦是0，即sin ＝0．同理，圆的的长是，所对圆心角的正弦是1，可记作sin ＝1．这一思想将线段与弧的度量单位统一起来，大大简化了某些三角公式及计算．

三、弧度制的正式提出——汤姆生

1873年6月5日，数学教师汤姆生(James Thomson)在北爱尔兰首府贝尔法斯特(Belfast)女王学院的数学考试题目中创造性地首先使用了“弧度”一词．当时，他将“半径”(radius)的前四个字母与“角”(angle)的前两个字母合在一起，构成radian，并被人们广泛接受和引用．我国学者曾把radian译成“弪’(由“弧”与“径”两字的一部分拼成)．中华人民共和国成立以来，中学数学教科书中都把radian译作“弧度”．

1881年，学者哈尔斯特(G．B．Halsted)等用希腊字母ρ表示弧度的单位，例如用表示弧度．1907年，学者包尔（G．N．Bauer)用r表示；1909年，学者霍尔(A．G．Hall)等又用R来表示，例如将弧度写成．现在人们习惯把弧度的单位省略．

弧度制的定义

等于半径长的圆弧所对的圆心角叫做1弧度的角，用弧度作单位来度量角的制度叫做弧度制。

以已知角a的顶点为圆心，以任意值R为半径作圆弧，则a角所对的弧长与R之比是一个定值﹝与R无关﹞，我们称=R时的正角为1弧度的角。以1弧度角为量角大小的单位，称此度量制为弧度制，以示与角的另一种度量制──角度制区别。

弧度制的基本思想

弧度制的基本思想是使圆半径与圆周长有同一度量单位，然后用对应的弧长与圆半径之比来度量角度，这一思想的雏型起源于印度。印度著名数学家阿利耶毗陀﹝476？-550？﹞定圆周长为21600分，相度地定圆半径为3438分﹝即取圆周率π3.142﹞，但阿利耶毗陀没有明确提出弧度制这个概念。严格的弧度概念是由瑞士数学家欧拉﹝1707-1783﹞于1748年引入。欧拉与阿利耶毗陀不同，先定半径为1个单位，那么半圆的弧长为π，此时的正弦值为0，就记为sinπ= 0，同理，1/4圆周的弧长为π/2，此时的正弦为1，记为sin(π/2)=1。从而确立了用π、π/2分别表示半圆及1/4圆弧所对的中心角。其它的角也可依此类推。

弧度制的精髓

弧度制的精髓就在于统一了度量弧与半径的单位，从而大大简化了有关公式及运算，尤其在高等数学中，其优点就格外明显。

1弧度的大小

一弧度的角：等于半径长的圆弧所对的圆心角叫做1弧度的角。

1弧度约等于57.3°

大约是57°17′45″

但准确的是等于180°/π

180°=πrad

利用弧度制证明扇形面积公式S=1/2LR.其中L是扇形的弧长,R是圆的半径

弧度制与角度制的换算公式

1 rad =180/π °

1°=π/180 rad