零、写在前面

这只是闲着没事随便写着玩的，大家随便看看就行。

一、基本定义

设角 $\alpha$ 的终边与单位圆交于点 $P(x,y)$ ,则有

$\sin \alpha=y$ , $\cos \alpha=x$

$\tan \alpha =\frac{y}{x}$ , $\cot\alpha=\frac{x}{y}$

$\sec \alpha=\frac{1}{x}$ , $\csc\alpha=\frac{1}{y}$

二、同角三角函数基本关系

由上边的式子可以直接得出以下三个关系式（倒数关系）：

$\tan\alpha\cot\alpha=1$
$\sin\alpha\csc\alpha=1$
$\cos\alpha\sec\alpha=1$
还可以得出如下商的关系：

$\frac{\sin\alpha}{\cos\alpha} =\tan\alpha=\frac{\sec\alpha}{\csc\alpha}$ $\frac{\cos\alpha}{\sin\alpha}=\cot\alpha=\frac{\csc\alpha}{\sec\alpha}$
结合勾股定理，我们还可以得到下述平方关系：

$\sin^{2}\alpha+\cos^{2}\alpha=1$
这些关系式很简单，就不推导了。

三、特殊值

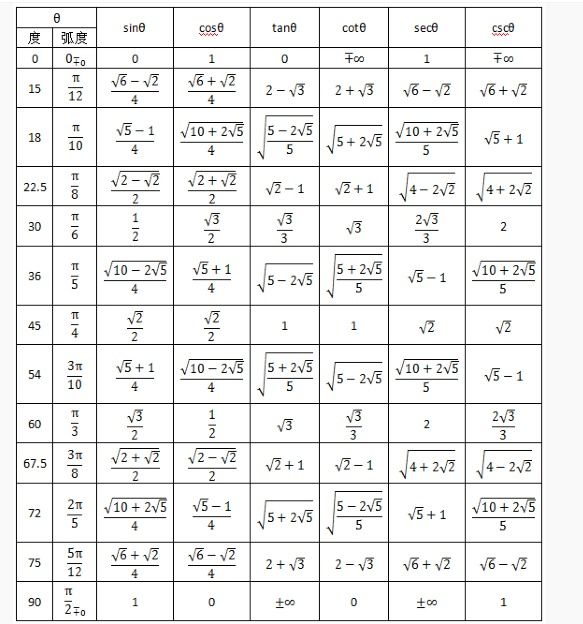
当这篇文章读完之后，你一定可以推导出上表中任何一个值。

四、诱导公式

我不推荐大家记这个表

而是希望大家先熟悉一下最基本的三个三角函数（sin、cos和tan）的性质，然后再讨论遇到类似问题如何最快速地推导。

正弦函数是奇函数，最小正周期为 $2\pi$ ,其导函数为余弦函数；
余弦函数是偶函数，最小正周期为 $2\pi$ ,其导函数为正弦函数的相反数；
正切函数是奇函数，最小正周期为 $\pi$ .

诱导公式的目的是什么呢？就是将 $\sin(\frac{k\pi}{2}+\alpha)$ 中 $\frac{\pi}{2}$ 的整数倍去掉，仅保留 $\alpha$ .因此我们可以按照上述性质一步步地化简：

按照其奇偶性，将 $\alpha$ 变为负值；
根据正弦/余弦函数的周期性，将 $2\pi$ 的整数倍全部去掉。若此时被加数为负，则再加上 $2\pi$ ；
若被加的数绝对值仍不小于 $\pi$ ，就将其绝对值直接减去 $\pi$ ，然后取负号；
利用公式 $\sin(\frac{\pi}{2} -\alpha)=\cos\alpha$ 和 $\cos(\frac{\pi}{2} -\alpha)=\sin\alpha$ 得出结果。

举个例子： $\cos(\frac{37\pi}{2} +\alpha)$

原式= $\cos(-\frac{37\pi}{2} -\alpha)$ /*将 $\alpha$ 变为负值*/

= $\cos(-\frac{\pi}{2} -\alpha)$ /*利用周期性加上9个 $2\pi$ */

= $\cos(\frac{3\pi}{2}-\alpha)$ /*再加上一个 $2\pi$ */

= $-\cos(\frac{\pi}{2}-\alpha)$ /*减去 $\pi$ 并加负号*/

= $-\sin\alpha$

可以看出，按照这个步骤，完全不需要记忆那么多公式，甚至连「奇变偶不变，负号看象限」都不需要，只要按部就班地做就可以得到正确答案。

而正切函数更简单，因为其最小正周期是 $\pi$ ,因此最后只有加不加 $\frac{\pi}{2}$ 的问题。

五、基本公式

下面看一个最基本的公式，这个公式很自然，但是确实下边各个公式推导的基础。

平面上两个单位向量，与x轴正向夹角分别为x和y，则这两个向量分别为 $(\cos x,\sin x)$ , $(\cos y,\sin y)$ 。则这两个向量的点积为 $\cos x\cos y+\sin x\sin y$ ,而点积又可以表示为 $1*1*\cos(x-y)=\cos(x-y)$ ,于是我们得到了以下公式：

$\cos(x-y)=\cos x\cos y+\sin x\sin y$ (1)

这就是最基本的公式。从向量的角度，这个公式也是很自然的。

六、和差角公式

将(1)中的 $y$ 用 $-y$ 代入，即可得到 $\cos(x+y)=\cos x\cos y-\sin x\sin y$ (2)

将(1)中的 $x$ 用 $\frac{\pi}{2} -x$ 代，再利用诱导公式，可以得到正弦函数的和差角公式：

$\sin(x+y)=\cos y\sin x+\cos x\sin y$ (3)

(3)式的 $y$ 代成 $-y$ ，有

$\sin(x-y)=\cos y\sin x-\cos x\sin y$ (4)

(3)/(2),(4)/(1),得到正切函数的和差角公式：

$\tan(x+y)=\frac{\tan x+\tan y}{1-\tan x\tan y}$ (5)

$\tan(x-y)=\frac{\tan x-\tan y}{1+\tan x\tan y}$ (6)

七、倍角公式和半角公式

有了「六」中的式子，令 $x=y$ ，很容易得到倍角公式和半角公式：

$\sin 2x=2\sin x\cos x$ (7)

$\cos 2x=\cos^{2}x-\sin^{2}x$ (8)

$\tan 2x=\frac{2\tan x}{1-\tan^{2}x}$ (9)

注意到(8)式，由平方关系又可以写成 $2\cos^{2}x-1$ 或 $1-2\sin^{2}x$ .所以我们就有半角公式（也叫降幂公式）：

$\sin^{2}\frac{x}{2}=\frac{1-\cos x}{2}$ (10)

$\cos^{2}\frac{x}{2}=\frac{1+\cos x}{2}$ (11)

两式相除，得

$\tan^{2}\frac{x}{2}=\frac{1-\cos x}{1+\cos x}$ (12)

八、积化和差和和差化积公式

回头看看(3)式和(4)式，两式相加得到

$\sin x\cos y=\frac{1}{2}[\sin(x+y)+\sin(x-y)]$ (13)

而相减则得

$\cos x\sin y=\frac{1}{2}[\sin(x+y)-\sin(x-y)]$ (14)

(1)+(2)、(1)-(2)同样可以得到两个积化和差的公式：

$\cos x\cos y=\frac{1}{2}[\cos(x+y)+\cos(x-y)]$ (15)

$\sin x\sin y=\frac{1}{2}[\cos(x-y)-\cos(x+y)]$ (16)

然后在上式中，令 $u=x+y,v=x-y$ .此时 $x=\frac{u+v}{2},y=\frac{u-v}{2}$ ，立刻就得到了四个和差化积公式：

$\sin u+\sin v=2\sin\frac{u+v}{2}\cos\frac{u-v}{2}$ (17)

$\sin u-\sin v=2\cos\frac{u+v}{2}\sin\frac{u-v}{2}$ (18)

$\cos u+\cos v=2\cos\frac{u+v}{2}\cos\frac{u-v}{2}$ (19)

$\cos u-\cos v=-2\sin\frac{u+v}{2}\sin\frac{u-v}{2}$ (20)

九、万能公式

万能公式是将 $\sin x,\cos x$ 和 $\tan x$ 均用 $\tan \frac{x}{2}$ 表示。由于后者的值域为整个实数区间，因此方便考察许多性质。

首先我们知道， $\tan x$ 的万能公式就是其二倍角公式(9)式。我们试着推导一下余弦函数的万能公式。

$\cos x=&\cos(2\cdot \frac{x}{2})=\cos^{2}\frac{x}{2}-\sin^{2}\frac{x}{2}=[\cos^{2}\frac{x}{2}-\sin^{2}\frac{x}{2}]/[\cos^{2}\frac{x}{2}+\sin^{2}\frac{x}{2}]$
$=\frac{1-\tan^{2}\frac{x}{2}}{1+\tan^{2}\frac{x}{2}}$ (21)

正弦的就简单了，两个一乘就行：

$\sin x=\cos x\tan x=\frac{1-\tan^{2}\frac{x}{2}}{1+\tan^{2}\frac{x}{2}}\frac{2\tan \frac{x}{2}}{1-\tan^{2}\frac{x}{2}}=\frac{2\tan x}{1-\tan^{2}x}$ (22)

十、写在最后

这篇文章实在是没什么技术含量，然而仓促之间我也写不出什么更好的东西了，大家凑合着看吧。

来源： https://zhuanlan.zhihu.com/p/20102140

----------------

来个土方法吧，亲测洗脑，高中老师讲了一次至今没忘过。。。

和差化积公式

如果把sin想象成笑(smile)，cos想象成哭(cry)，那么口诀就有了：

-------------

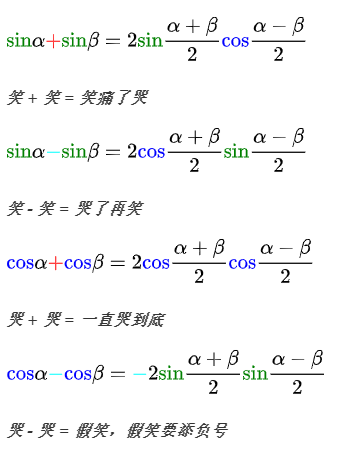
前阵子出过一道（），有一些网友踊跃提供了自己的思路。在公布我的做法之前，我想先讲讲其中需要利用到的一个有关三角函数的公式以及其证明，大家可以先了解一下三角函数的定义：

先来看看两角和差的三角函数公式的内容吧，真是又对称又神奇吧：

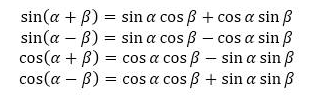
证明方法并不唯一，在这里提供一种我认为比较容易理解的方法。如下图所示，从 A 出发作 ∠α 和 ∠β，在 ∠β 的一条射线上取一点 D ，过 D 作 ∠β 的另一条射线的垂线，设垂足为 E。然后过 E 作∠α 的另一条射线的垂线，设垂足为 B。再延长 EB，作 CD ⊥ CE。

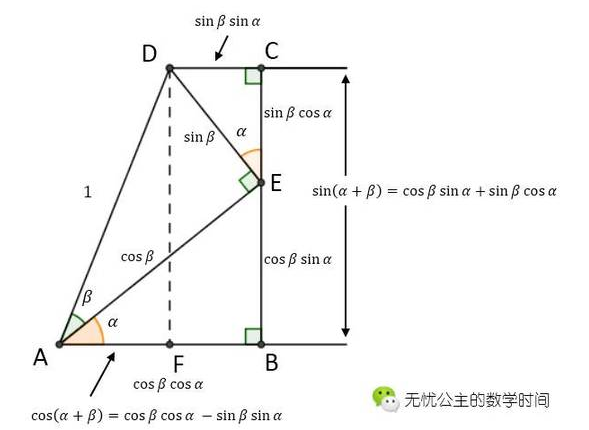
如果假设 AD = 1，那么在 △AED 中，AE = cosβ，DE = sinβ。先来证明第 1 个公式：在 △CDE 中，CE = sinβ cosα；在 △ABE 中，BE = cosβ sinα；在 △ADF 中，DF = sin ( α+β )。因为 DF = BC = BE + CE，所以 sin ( α+β ) = cosβ sinα + sinβ cosα。如果需要证明第 2 个式子，可将 -β 看作一个整体代入第 1 个式子。

然后我们用类似的办法证明第 3 个式子：在 △ABE 中，AB = cosβ cosα；在 △CDE 中，CD = sinβ sinα；在 △AFD 中，AF = cos( α+β ) 。因为 AF = AB – CD，所以 cos ( α+β ) = cos β cosα – sinβ sinα。同理，如果需要证明第 4 个式子，可将 -β 看作一个整体代入第 3 个式子。

不过这个两角和差的三角函数公式有什么用呢？敬请期待烧脑几何题 142 的解题思路吧！

----------------------

万能三角函数公式

(1)(sinα)^2+(cosα)^2=1

(2)1+(tanα)^2=(secα)^2

(3)1+(cotα)^2=(cscα)^2

证明下面两式，只需将一式，左右同除(sinα)^2,第二个除(cosα)^2即可

(4)对于任意非直角三角形，总有tanA+tanB+tanC=tanAtanBtanC

设tan(A/2)=t

sinA=2t/(1+t^2) （A≠2kπ+π，k∈Z）

tanA=2t/(1-t^2) （A≠2kπ+π，k∈Z）

cosA=(1-t^2)/(1+t^2) （A≠2kπ+π k∈Z）