来源:互联网
Queue
------------
1.ArrayDeque,
2.PriorityQueue,
3.ConcurrentLinkedQueue,
4.DelayQueue,
5.ArrayBlockingQueue,
6.LinkedBlockingQueue,
7.LinkedBlockingDeque
8.PriorityBlockingQueue,
9.SynchronousQueue
------------
---------------------------------------
PriorityQueue(优先级队列)
/**
*PriorityQueue是一个优先级堆(二叉堆)的无界优先级队列。
*优先级队列的元素按照其自然顺序(Comparable)进行排序,或者根据构造队列时提供的Comparator进行排序,具体取决于所使用的构造方法。
*优先级队列不允许使用null元素。依靠自然顺序的优先级队列还不允许插入不可比较的对象(否则会导致ClassCaseException)。
*此队列的头是按指定排序方式确定的最小元素。如果多个元素都是最小值,则头是其中一个元素--选择方法是任意的。
*队列获取操作 poll、remove、peek和element访问处于队列头的元素。
*优先级队列是无界的,但是有一个内部容量,控制着用于存储队列元素的数组大小。它至少等于队列的大小。随着不断向优先级队列
*添加元素,其容量会自动增加。无需指定容量增加策略的细节。
*/
public class PriorityQueue<E> extends AbstractQueue<E> implements java.io.Serializable {
private static final int DEFAULT_INITIAL_CAPACITY = 11;//默认的初始容量为11
/**
* 优先队列是通过“平衡二叉堆”的形式实现的:
* 对于数组queue中任一元素queue[n],其左儿子为queue[2*n+1],右儿子为queue[2*(n+1)];
* 优先级队列的元素按照其自然顺序(Comparable)进行排序,或者根据构造队列时提供的Comparator进行排序,
* 具体取决于所使用的构造方法。
* 在堆中,对于每个节点n,n的父节点中的关键字小于或等于n中的关键字,根节点也就是queue[0]是最小的。
*/
private transient Object[] queue;
private int size = 0;//优先级队列中元素的个数
/**
* 节点的关键字“比较器”,如果为null则采用关键字的自然排序(Comparable)方式
*/
private final Comparator<? super E> comparator;
/**
* 优先队列结构变动的次数
*/
private transient int modCount = 0;
/**
* 无参构造,采用默认容量及元素的自然排序(Comparable)形式
*/
public PriorityQueue() {
this(DEFAULT_INITIAL_CAPACITY, null);
}
/**
* 指定容量
*/
public PriorityQueue(int initialCapacity) {
this(initialCapacity, null);
}
/**
* 指定容量及排序器
*/
public PriorityQueue(int initialCapacity, Comparator<? super E> comparator) {
// Note: This restriction of at least one is not actually needed,
// but continues for 1.5 compatibility
if (initialCapacity < 1)
throw new IllegalArgumentException();
this.queue = new Object[initialCapacity];
this.comparator = comparator;
}
/**
* 通过“集合”初始化队列并根据集合的类型初始化排序器
*/
public PriorityQueue(Collection<? extends E> c) {
initFromCollection(c);
if (c instanceof SortedSet)
comparator = (Comparator<? super E>)
((SortedSet<? extends E>)c).comparator();
else if (c instanceof PriorityQueue)
comparator = (Comparator<? super E>)
((PriorityQueue<? extends E>)c).comparator();
else {
comparator = null;
heapify();
}
}
/**
* 通过另一个“优先队列”初始化队列及其排序方式
*/
public PriorityQueue(PriorityQueue<? extends E> c) {
comparator = (Comparator<? super E>)c.comparator();
initFromCollection(c);
}
/**
* 通过“排序集合”初始化队列及其排序方式
*/
public PriorityQueue(SortedSet<? extends E> c) {
comparator = (Comparator<? super E>)c.comparator();
initFromCollection(c);
}
/**
* 通过集合初始化数组
*/
private void initFromCollection(Collection<? extends E> c) {
Object[] a = c.toArray();
// If c.toArray incorrectly doesn't return Object[], copy it.
if (a.getClass() != Object[].class)
a = Arrays.copyOf(a, a.length, Object[].class);
queue = a;
size = a.length;
}
/**
*增加数组容量
*/
private void grow(int minCapacity) {
if (minCapacity < 0) // overflow
throw new OutOfMemoryError();
int oldCapacity = queue.length;
// Double size if small; else grow by 50%
int newCapacity = ((oldCapacity < 64)?
((oldCapacity + 1) * 2):
((oldCapacity / 2) * 3));
if (newCapacity < 0) // overflow
newCapacity = Integer.MAX_VALUE;
if (newCapacity < minCapacity)
newCapacity = minCapacity;
queue = Arrays.copyOf(queue, newCapacity);
}
/**
* 插入元素
*/
public boolean add(E e) {
return offer(e);
}
/**
* 插入元素
*/
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length)
grow(i + 1);//增加容量
size = i + 1;
if (i == 0)//如果插入前为空队列
queue[0] = e;
else
siftUp(i, e);//通过堆的“上滤”方式插入新的元素(i是最后一个元素的位置)
return true;
}
//获得队头元素
public E peek() {
if (size == 0)
return null;
return (E) queue[0];
}
//遍历得到元素o的索引
private int indexOf(Object o) {
if (o != null) {
for (int i = 0; i < size; i++)
if (o.equals(queue[i]))
return i;
}
return -1;
}
/**
* 删除元素(通过equals的方式)
*/
public boolean remove(Object o) {
int i = indexOf(o);
if (i == -1)
return false;
else {
removeAt(i);
return true;
}
}
/**
* 删除元素(通过==(引用相等)的方式)
*/
boolean removeEq(Object o) {
for (int i = 0; i < size; i++) {
if (o == queue[i]) {
removeAt(i);
return true;
}
}
return false;
}
/**
* 是否包含
*/
public boolean contains(Object o) {
return indexOf(o) != -1;
}
/**
* 返回队列元素的Object数组
*/
public Object[] toArray() {
return Arrays.copyOf(queue, size);
}
/**
* 返回指定返回类型队列元素的数组
*/
public <T> T[] toArray(T[] a) {
if (a.length < size)
// Make a new array of a's runtime type, but my contents:
return (T[]) Arrays.copyOf(queue, size, a.getClass());
System.arraycopy(queue, 0, a, 0, size);
if (a.length > size)
a[size] = null;
return a;
}
//遍历器
public Iterator<E> iterator() {
return new Itr();
}
private final class Itr implements Iterator<E> {
……
}
public int size() {
return size;
}
/**
* 清空队列
*/
public void clear() {
modCount++;
for (int i = 0; i < size; i++)
queue[i] = null;
size = 0;
}
//出对
public E poll() {
if (size == 0)
return null;
int s = --size;//最后一个元素索引
modCount++;
E result = (E) queue[0];
E x = (E) queue[s];
queue[s] = null;
if (s != 0)
siftDown(0, x);//安排最后一个元素的位置
return result;
}
/**
* 删除指定位置的元素
*/
private E removeAt(int i) {
assert i >= 0 && i < size;
modCount++;
int s = --size;
if (s == i) // 如果是最后一个元素,直接删除
queue[i] = null;
else { //否则,还要考虑删除位置i元素后,最后一个元素重新安排位置的问题
E moved = (E) queue[s];
queue[s] = null;
siftDown(i, moved);//“下滤”策略
if (queue[i] == moved) {//为了应对“迭代器”执行期间进行的remove操作,而导致的“Unlucky”元素设置的。
siftUp(i, moved);
if (queue[i] != moved)
return moved;
}
}
return null;
}
/**
*优先队列的“插入操作”时调用该“上滤”策略 :(主要是安排“插入的新元素”的合适位置)
*为了将一个元素x插入到堆中,我们在下一个可用位置(就是最后一个叶子节点的下一个节点处)
*创建一个空穴,否则该堆不是完全树。如果x可以放在该空穴中并不破坏堆的序,那么就插入完成。
*否则,我们把空穴的父节点上的元素移入空穴中,这样空穴就朝着根的方向向上冒一步。继续改过程
*直到x能被放入空穴中为止。
*
* 也就是,从位置k(该类中传入的k为最后一个元素的位置)处插入元素x,为了保证堆序性质,
* 就对x进行“上滤”操作直到x为叶子节点或者小于等于它的孩子节点。
*/
private void siftUp(int k, E x) {
if (comparator != null)//比较器为null时
siftUpUsingComparator(k, x);
else
siftUpComparable(k, x);
}
//“上滤”策略,通过自然顺序比较关键字
private void siftUpComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x;
while (k > 0) {
int parent = (k - 1) >>> 1;//父位置
Object e = queue[parent];
if (key.compareTo((E) e) >= 0)//key>=父时,就表示该位置适合插入,
break;
//key比父小时,父就下移,k指定到原来父的位置,继续“上移”循环,直到key>=父或者k=0(为根)
queue[k] = e;
k = parent;
}
queue[k] = key;
}
//“上滤”策略,通过比较器比较关键字
private void siftUpUsingComparator(int k, E x) {
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = queue[parent];
if (comparator.compare(x, (E) e) >= 0)
break;
queue[k] = e;
k = parent;
}
queue[k] = x;
}
/**
*优先队列(二叉堆)的“删除操作”时调用该“下滤”策略 :(主要是安排最后一个元素的位置)
*当删除一个最小元时,要在根节点建立一个空穴。由于现在少了一个元素,因此堆中最后一个元素x必须移动到某个
*位置。如果x可以放在空穴中,那么操作结束,否则将空穴的两个儿子中的较小者移入空穴,这样空穴就向下推进一层。
*重复该步骤直到x可以被放入空穴中。因此,我们的做法就是将x置于沿着k开始包含最小儿子的一条路径上的一个正确
*位置。
* 优先队列(小顶堆)的删除操作一般指的删除最小元(堆顶,根节点),当然也可以是k位置。
* 也就是把位置k处设为空穴,对(最后一个元素)x进行“下滤”操作 直到x为叶子节点或者小于等于它的孩子节点。
*/
private void siftDown(int k, E x) {
if (comparator != null)
siftDownUsingComparator(k, x);
else
siftDownComparable(k, x);
}
//“下滤”操作,通过关键字的comparable比较元素大小
private void siftDownComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>)x;
int half = size >>> 1; // 循环非叶子节点(因为最后一个元素位于叶子节点处,只在叶子节点以上的部分寻找)
while (k < half) {//k是指删除的元素的位置
int child = (k << 1) + 1; // 左儿子位置
Object c = queue[child];
int right = child + 1; // 右儿子位置
//如果右儿子不是最后一个节点,c指向小节点
if (right < size &&
((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
c = queue[child = right];
if (key.compareTo((E) c) <= 0)//如果key不大于其孩子节点,说明该空穴位置k可以插入了
break;
//如果key>它的最小子节点c,就“下滤”循环
queue[k] = c;
k = child;
}
queue[k] = key;
}
//“下滤”操作,通过Comparator(比较器)比较元素大小
private void siftDownUsingComparator(int k, E x) {
int half = size >>> 1;
while (k < half) {
int child = (k << 1) + 1;
Object c = queue[child];
int right = child + 1;
if (right < size &&
comparator.compare((E) c, (E) queue[right]) > 0)
c = queue[child = right];
if (comparator.compare(x, (E) c) <= 0)
break;
queue[k] = c;
k = child;
}
queue[k] = x;
}
……
}
在堆排序这篇文章中千辛万苦的实现了堆的结构和排序,其实在Java 1.5版本后就提供了一个具备了小根堆性质的数据结构也就是优先队列PriorityQueue。下面详细了解一下PriorityQueue到底是如何实现小顶堆的,然后利用PriorityQueue实现大顶堆。
PriorityQueue的数据结构
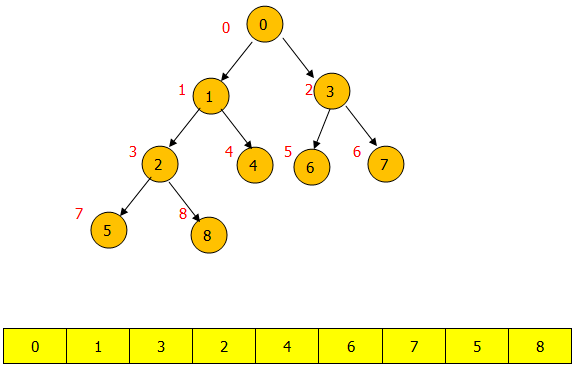
PriorityQueue的逻辑结构是一棵完全二叉树,存储结构其实是一个数组。逻辑结构层次遍历的结果刚好是一个数组。
PriorityQueue的操作
①add(E e) 和 offer(E e) 方法
add(E e) 和 offer(E e) 方法都是向PriorityQueue中加入一个元素,其中add()其实调用了offer()方法如下:
public boolean add(E e) {
return offer(e);
}下面主要看看offer()方法的作用:
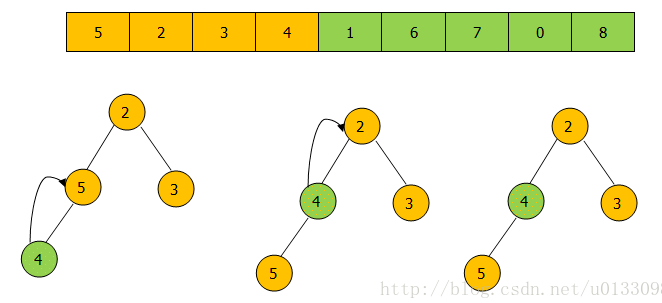
如上图调用 offer(4)方法后,往堆中压入4然后从下往上调整堆为小顶堆。offer()的代码实现:
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
//如果压入的元素为null 抛出异常
int i = size;
if (i >= queue.length)
grow(i + 1);
//如果数组的大小不够扩充
size = i + 1;
if (i == 0)
queue[0] = e;
//如果只有一个元素之间放在堆顶
else
siftUp(i, e);
//否则调用siftUp函数从下往上调整堆。
return true;
}对上面代码做几点说明:
①优先队列中不能存放空元素。
②压入元素后如果数组的大小不够会进行扩充,上面的queue其实就是一个默认初始值为11的数组(也可以赋初始值)。
③offer元素的主要调整逻辑在 siftUp ( i, e )函数中。下面看看 siftUp(i, e) 函数到底是怎样实现的。
private void siftUpComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x;
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = queue[parent];
if (key.compareTo((E) e) >= 0)
break;
queue[k] = e;
k = parent;
}
queue[k] = key;
}
上面的代码还是比较简明的,就是当前元素与父节点不断比较如果比父节点小就交换然后继续向上比较,否则停止比较的过程。
② poll() 和 remove() 方法
poll 方法每次从 PriorityQueue 的头部删除一个节点,也就是从小顶堆的堆顶删除一个节点,而remove()不仅可以删除头节点而且还可以用 remove(Object o) 来删除堆中的与给定对象相同的最先出现的对象。先看看poll()方法。下面是poll()之后堆的操作
删除元素后要对堆进行调整:
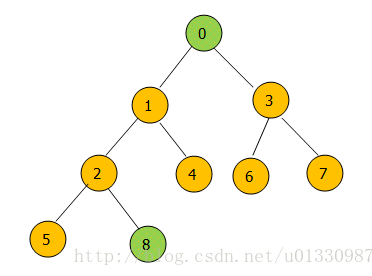
堆中每次删除只能删除头节点。也就是数组中的第一个节点。
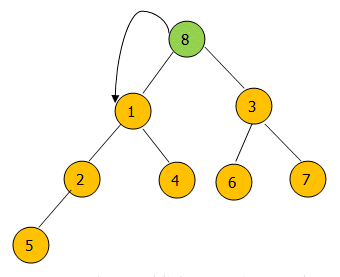
将最后一个节点替代头节点然后进行调整。
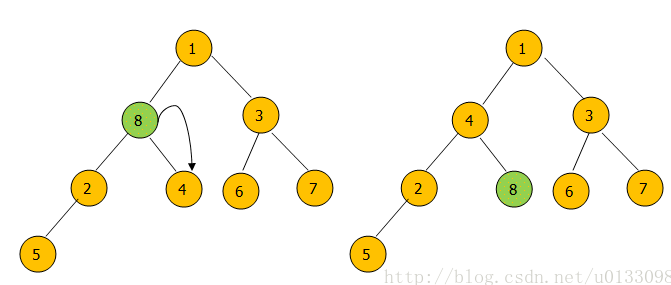
如果左右节点中的最小节点比当前节点小就与左右节点的最小节点交换。直到当前节点无子节点,或者当前节点比左右节点小时停止交换。
poll()方法的源码
public E poll() {
if (size == 0)
return null;
//如果堆大小为0则返回null
int s = --size;
modCount++;
E result = (E) queue[0];
E x = (E) queue[s];
queue[s] = null;
//如果堆中只有一个元素直接删除
if (s != 0)
siftDown(0, x);
//否则删除元素后对堆进行调整
return result;
}看看 siftDown(0, x) 方法的源码:
private void siftDownComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>)x;
int half = size >>> 1; // loop while a non-leaf
while (k < half) {
int child = (k << 1) + 1; // assume left child is least
Object c = queue[child];
int right = child + 1;
if (right < size &&
((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
c = queue[child = right];
if (key.compareTo((E) c) <= 0)
break;
queue[k] = c;
k = child;
}
queue[k] = key;
}siftDown()方法就是从堆的第一个元素往下比较,如果比左右孩子节点的最小值小则与最小值交换,交换后继续向下比较,否则停止比较。
remove(4)的过程图:
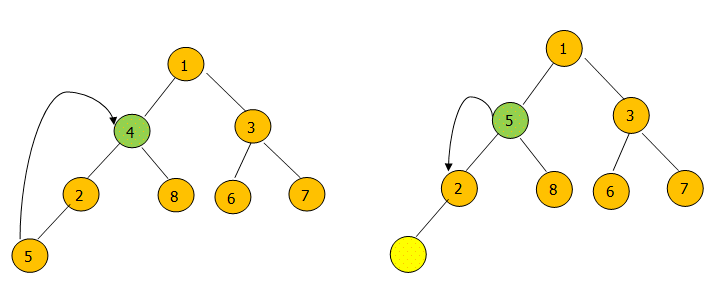
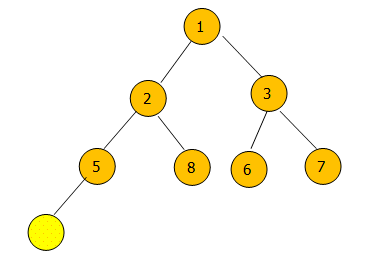
先用堆的最后一个元素 5 代替4然后从5开始向下调整堆。这个过程和poll()函数一样,只不过poll()函数每次都是从堆顶开始。
remove(Object o)的代码:
public boolean remove(Object o) {
int i = indexOf(o);
//先在堆中找到o的位置
if (i == -1)
return false;
//如果不存在则返回false。
else {
removeAt(i);
//否则删除数组中第i个位置的值,调整堆。
return true;
}
}removeAt(int i)的代码
private E removeAt(int i) {
assert i >= 0 && i < size;
modCount++;
int s = --size;
if (s == i) // removed last element
queue[i] = null;
else {
E moved = (E) queue[s];
queue[s] = null;
siftDown(i, moved);
if (queue[i] == moved) {
siftUp(i, moved);
if (queue[i] != moved)
return moved;
}
}
return null;
}使用PriorityQueue实现大顶堆
PriorityQueue默认是一个小顶堆,然而可以通过传入自定义的Comparator函数来实现大顶堆。如下代码:
private static final int DEFAULT_INITIAL_CAPACITY = 11;
PriorityQueue<Integer> maxHeap=new PriorityQueue<Integer>(DEFAULT_INITIAL_CAPACITY, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
});实现了一个初始大小为11的大顶堆。这里只是简单的传入一个自定义的Comparator函数,就可以实现大顶堆了。
来源: https://blog.csdn.net/u013309870/article/details/71189189