来源:互联网
1.熟悉点估计概念与操作方法
2.熟悉区间估计的概念与操作方法
3.熟练掌握T检验的SPSS操作
4.学会利用T检验方法解决身边的实际问题
1.参数估计的基本原理
2.假设检验的基本原理
1.单个总体均值的区间估计
例题:为研究在黄金时段中,即每晚8:30-9:00 内,电视广告所占时间的多少。美国广告协会抽样调查了20个最佳电视时段中广告所占的时间(单位:分钟)。请给出每晚8:30 开始的半小时内广告所占时间区间估计,给定的置信度为95%。 操作程序:
- 打开SPSS,建立数据文件:“ 电视节目市场调查.sav”。这里,研究变量为:time,即每天看电视的时间。
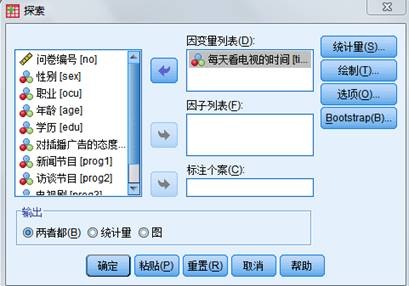
- 选择区间估计选项,方法如下: 选择菜单【分析】—>【描述统计】—>【探索】” ,打开图3.1Explore 对话框。
- 从源变量清单中将“time”变量移入Dependent List框中。
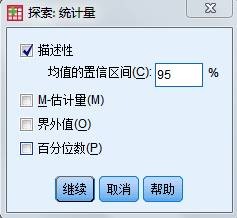
- 单击上图右方的“统计量”按钮打开“探索:统计量”对话框。在设置均值的置信水平,如键入95%,完成后单击“继续”按钮回到主窗口。
- 返回主窗口点击ok运行操作。
- 计算结果简单说明:
表3.1 描述统计量
Descriptives
Statistic | Std. Error | |||
time | Mean | 6.5350 | .13480 | |
95% Confidence Interval for Mean | Lower Bound | 6.2529 | ||
Upper Bound | 6.8171 | |||
5% Trimmed Mean | 6.5167 | |||
Median | 6.4500 | |||
Variance | .363 | |||
Std. Deviation | .60287 | |||
Minimum | 5.60 | |||
Maximum | 7.80 | |||
Range | 2.20 | |||
Interquartile Range | .95 | |||
Skewness | .295 | .512 | ||
Kurtosis | -.612 | .992 |
- 如上表显示。从上表“ 95% Confidence Interval for Mean ”中可以得出,每晚8:30 开始的半小时内广告所占时间区间估计(置信度为95%) 为:(6.2529,6.8171),其中lower Bound 表示置信区间的下限,Upper Bound表示置信区间的上限。点估计是:6.5350。
2.两个总体均值之差的区间估计
例题:The Wall Street Journal(1994,7 )声称在制造业中,参加工会的妇女比未参加工会的妇女的报酬要多2.5 美元。想通过统计方法,对这个观点是否正确给出检验。
假设抽取了7位女性工会会员与8位非工会会员女性报酬数据。要求对制造业中参加工会会员的女性报酬与未参加工会的女性报酬平均工资之差进行区间估计,预设的置信度为95%。
- 打开SPSS,按如下图示格式输入原始数据,建立数据文件:“工会会员工资差别.spss”。这里,“会员”表示是否为工会会员的变量,y 表示是工会会员,n表示非工会会员,“报酬”表示女性员工报酬变量,单位:千美元。
- 计算两总体均值之差的区间估计,采用“独立样本T 检验”方法。选择菜单“ 【分析】→【比较均值】→独立样本T检验”, 打开对话框。
- 变量选择
(1)从源变量清单中将“报酬”变量移入检验变量框中。表示要求该变量的均值的区间估计。
(2)从源变量清单中将“group”变量移入分组变量框中。表示总体的分类变量。 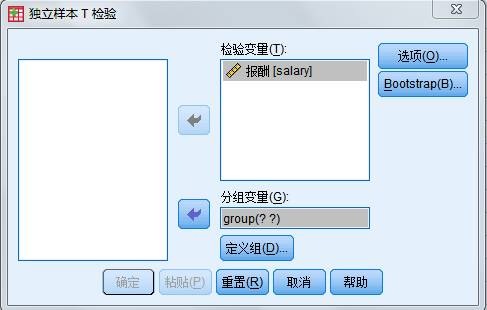
图3.3 独立样本T检验 对话框
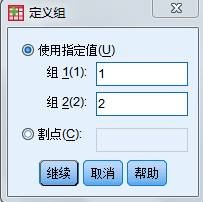
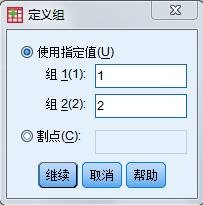
- 定义分组 单击定义组按钮,打开Define Groups 对话框。在Group1 中输入1,在Group2 中输入2(1表示非工会会员,2 表示工会会员)。完成后单击“继续”按钮回到主窗口。
- 计算结果 单击上图中“OK”按钮,输出结果如下图所示。
(1)Group Statistics(分组统计量)表
分别给出不同总体下的样本容量、均值、标准差和平均标准误。从该表中可以看出,参加工会的妇女平均报酬为19.925,不参加工会的妇女平均报酬为20.1429。
表3.2 分组统计量
Group Statistics
会员 | N | Mean | Std. Deviation | Std. Error Mean | ||
报酬 | 1.00 | 8 | 19.9250 | .46522 | .16448 | |
2.00 | 7 | 20.1429 | .52236 | .19743 |
(2)Independent Sample Test (独立样本T 检验)表
Levene’s Test for Equality of Variance,为方差检验,在Equal variances assumed (原假设:方差相等)下,F=0.623, 因为其P-值大于显著性水平,即:Sig.=0.444>0.05, 说明不能拒绝方差相等的原假设,接受两个总体方差是相等的假设。因此参加工会会员的女性报酬与未参加工会的女性报酬平均工资之差95%的区间估计为[0.76842,0.33271]。
T-test for Equality of Means 为检验总体均值是否相等的t 检验,由于在本例中,其P-值大于显著性水平,即:Sig.=0.408>0.05, 因此不应该拒绝原假设,也就是说参加工会的妇女跟未参加工会的妇女的报酬没有显著差异。本次抽样推断结论不支持The Wall Street Journal(1994,7 )提出的“参加工会的妇女比未参加工会的妇女的报酬要多2.5 美元”观点,即参加工会的妇女不比未参加工会的妇女的报酬多。
表3.3 独立样本T检验结果
Independent Samples Test
Levene's Test for Equality of Variances | t-test for Equality of Means | |||||||||
F | Sig. | t | df | Sig. (2-tailed) | Mean Difference | Std. Error Difference | 95% Confidence Interval of the Difference | |||
Lower | Upper | |||||||||
报酬 | Equal variances assumed | .623 | .444 | -.855 | 13 | .408 | -.21786 | .25485 | -.76842 | .33271 |
Equal variances not assumed | -.848 | 12.187 | .413 | -.21786 | .25697 | -.77679 | .34108 |
3.单个总体均值的假设检验 (单样本T检验)
例子:某种品牌的沐浴肥皂制造程序的设计规格中要求每批平均生产120 块肥皂,高于或低于该数量均被认为是不合理的,在由10 批产品所组成的一个样本中,每批肥皂的产量数据见下表,在0.05 的显著水平下,检验该样本结果能否说明制造过程运行良好?
- 判断检验类型 该例属于“大样本、总体标准差σ未知。假设形式为:
H0:μ=μ0, H1 :μ≠μ0
- 软件实现程序 打开已知数据文件,然后选择菜单“【分析】→【比较均值】→单样本T检验”,打开One-Sample T Test 对话框。从源变量清单中将“产品数量”向右移入“Test Variables”框中。
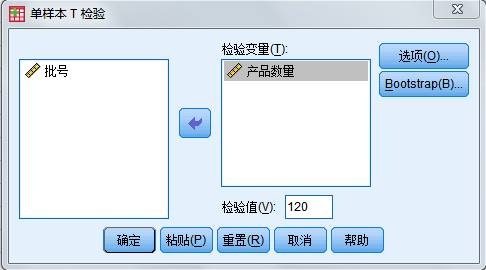
图3.5 one-sample T test窗口
在“Test Value” 框里输入一个指定值(即假设检验值,本例中假设为120),T 检验过程将对每个检验变量分别检验它们的平均值与这个指定数值相等的假设。
- “One-Sample T Test”窗口中“OK”按钮,输出结果如下表所示。
(1)“One-Sample Statistics”(单个样本的统计量)表 分别给出样本的容量、均值、标准差和平均标准误。本例中,产品数量均值为118.9000。
表3.4 单样本统计量
One-Sample Statistics
N | Mean | Std. Deviation | Std. Error Mean | |
产品数量 | 10 | 118.9000 | 4.93176 | 1.55956 |
(2)“One-Sample Test”(单个样本的检验)表 表中的t 表示所计算的T 检验统计量的数值,本例中为-0.705。 表中的“df”,表示自由度,本例中为9。 表中的“Sig”(双尾T 检验), 表示统计量的P-值, 并与双尾T检验的显著性的大小进行比较:Sig.=0.498>0.05,说明这批样本的平均产量与120 无显著差异。表中的“Mean Difference”, 表示均值差,即样本均值与检验值120 之差, 本例中为-1.1000。表中的“95% Confidence Internal of the Difference”, 样本均值与检验值偏差的95%置信区间为(-4.628,2.428),置信区间包括数值0,说明样本数量与120 无显著差异,符合要求。
表3.5 单样本T检验结果
One-Sample Test
Test Value = 120 | |||||||
t | df | Sig. (2-tailed) | Mean Difference | 95% Confidence Interval of the Difference | |||
Lower | Upper | ||||||
产品数量 | -.705 | 9 | .498 | -1.10000 | -4.6280 | 2.4280 |
4.两独立样本的假设检验(两独立样本T检验)
例题:The Wall Street Journal(1994,7 )声称在制造业中,参加工会的妇女比未参加工会的妇女的报酬要多2.5 美元。想通过统计方法,对这个观点是否正确给出检验。
假设抽取了7位女性工会会员与8位非工会会员女性报酬数据。要求对制造业中参加工会会员的女性报酬与未参加工会的女性报酬平均工资之差进行区间估计,预设的置信度为95%。
- 打开SPSS,按如下图示格式输入原始数据,建立数据文件:“工会会员工资差别.sav”。这里,“会员”表示是否为工会会员的变量,y 表示是工会会员,n表示非工会会员,“报酬”表示女性员工报酬变量,单位:千美元。
- 计算两总体均值之差的区间估计,采用“独立样本T 检验”方法。选择菜单“ 【分析】→【比较均值】→【独立样本T检验】”。
(1)从源变量清单中将“报酬”变量移入检验变量框中。表示要求该变量的均值的检验。
(2)从源变量清单中将“会员”变量移入分组变量框中。表示总体的分类变量。 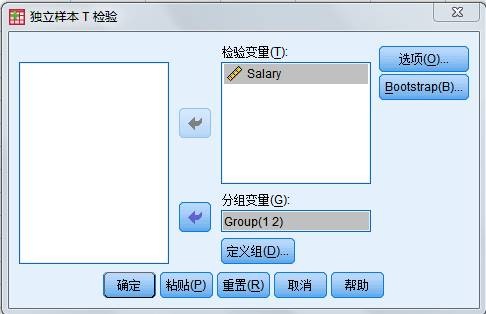
图3.6 sample T test 窗口
- 定义分组 单击Grouping Variable 框下面的Define Groups 按钮,打开Define Groups 对话框。在Group1 中输入1,在Group2 中输入2(1表示非工会会员,2 表示工会会员)。完成后单击“继续”按钮返回主窗口。
- 计算结果 单击上图中“OK”按钮,输出结果如下图所示。
(1)Group Statistics(分组统计量)表
分别给出不同总体下的样本容量、均值、标准差和平均标准误。从该表中可以看出,参加工会的妇女平均报酬为19.925,不参加工会的妇女平均报酬为20.1429。
表3.6 分组统计量
Group Statistics
会员 | N | Mean | Std. Deviation | Std. Error Mean | ||
报酬 | 1.00 | 8 | 19.9250 | .46522 | .16448 | |
2.00 | 7 | 20.1429 | .52236 | .19743 |
(2)Independent Sample Test (独立样本T 检验)表
Levene’s Test for Equality of Variance,为方差检验,在Equal variances assumed (原假设:方差相等)下,F=0.623, 因为其P-值大于显著性水平,即:Sig.=0.444>0.05, 说明不能拒绝方差相等的原假设,接受两个总体方差是相等的假设。
T-test for Equality of Means 为检验总体均值是否相等的t 检验,由于在本例中,其P-值大于显著性水平,即:Sig.=0.408>0.05, 因此不应该拒绝原假设,也就是说参加工会的妇女跟未参加工会的妇女的报酬没有显著差异。本次抽样推断结论不支持The Wall Street Journal(1994,7 )提出的“参加工会的妇女比未参加工会的妇女的报酬要多2.5 美元”观点,即参加工会的妇女不比未参加工会的妇女的报酬多。
表3.7 独立样本T检验结果
Independent Samples Test
Levene's Test for Equality of Variances | t-test for Equality of Means | |||||||||
F | Sig. | t | df | Sig. (2-tailed) | Mean Difference | Std. Error Difference | 95% Confidence Interval of the Difference | |||
Lower | Upper | |||||||||
报酬 | Equal variances assumed | .623 | .444 | -.855 | 13 | .408 | -.21786 | .25485 | -.76842 | .33271 |
Equal variances not assumed | -.848 | 12.187 | .413 | -.21786 | .25697 | -.77679 | .34108 |
5.配对样本T检验
配对样本是对应独立样本而言的,配对样本是指一个样本在不同时间做了两次试验,或者具有两个类似的记录,从而比较其差异;独立样本检验是指不同样本平均数的比较,而配对样本检验往往是对相同样本二次平均数的检验。
配对样本T检验的前提条件为:第一,两样本必须是配对的。即两样本的观察值数目相同,两样本的观察值顺序不随意更改。第二,样本来自的两个总体必须服从正态分布。例如针对试验前学习成绩何智商相同的两组学生,分别进行不同教学方法的训练,进行一段时间试验教学后,比较参与试验的两组学生的学习成绩是否存在显著性差异。
假设某校为了检验进行新式培训前后学生的学习成绩是否有了显著提高,从全校学生中随机抽出30名进行测试,这些学生培训前后的考试成绩放置于数据文件“学生培训.sav”中。在SPSS中对这30名学生的成绩进行配对样本t检验的操作步骤如下:
- 选择菜单【分析】→【比较均值】→【配对样本T检验】,打开对话框,如图3.8所示,将两个配对变量移入右边的Pair Variables列表框中。移动的方法是先选择其中的一个配对变量,再选择第二个配对变量,接着单击中间的箭头按钮。
- 选项按钮的用于设置置信度选项,这里保持系统默认的95%
- 在主对话框中单击ok按钮,执行操作。
- 实例结果分析
表3.8和表3.9给出了培训前后学生考试成绩的均值、标准差、均值标准误差以及培训前后成绩的相关系数。从表3.8来看,培训前后平均成绩并没有发生显著的提高。
表3.10给出了配对样本t检验结果,包括配对变量差值的均值、标准差、均值标准误差以及差值的95%置信度下的区间估计。当然也给出了最为重要的t统计量和p值。结果显示p=0.246>0.05,所以,学校的所谓新式培训并未带来学生成绩的显著变化。
表3.8 培训前后成绩的描述统计量
Paired Samples Statistics
Mean | N | Std. Deviation | Std. Error Mean | |||
Pair 1 | 培训前 | 67.00 | 30 | 14.734 | 2.690 | |
培训后 | 68.60 | 30 | 12.947 | 2.364 |
表3.9 培训前后成绩的相关系数
Paired Samples Correlations
N | Correlation | Sig. | ||
Pair 1 | 培训前&培训后 | 30 | .865 | .000 |
表3.10 配对样本T检验结果
Paired Samples Test
Paired Differences | t | df | Sig. (2-tailed) | ||||||
Mean | Std. Deviation | Std. Error Mean | 95% Confidence Interval of the Difference | ||||||
Lower | Upper | ||||||||
Pair 1 | 培训前-培训后 | -1.600 | 7.398 | 1.351 | -4.362 | 1.162 | -1.185 | 29 | .246 |
四、备择试验
1.某省大学生四级英语测验平均成绩为65,现从某高校随机抽取20份试卷,其分数为:72、76、68、78、62、59、64、85、70、75、61、74、87、83、54、76、56、66、68、62,问该校英语水平与全区是否基本一致?设α=0.05
2.分析某班级学生的高考数学成绩是否存在性别上的差异。数据如表所示:
某班级学生的高考数学成绩
性别 | 数学成绩 |
男(n=18) | 85 89 75 58 86 80 78 76 84 89 99 95 82 87 60 85 75 80 |
女(n=12) | 92 96 86 83 78 87 70 65 70 65 70 78 72 56 |
3.SPSS自带的数据文件world95.sav中,保存了1995年世界上109个国家和地区的部分指标的数据,其中变量“lifeexpf”,“lifeexpm”分别为各国或地区女性和男性人口的平均寿命。假设将这两个指标数据作为样本,试用配对样本T检验,女性人口的平均寿命是否确实比男性人口的平均寿命长,并给出差异的置信区间。(设α=0.05)