来源：互联网

一、试验目标与要求

本试验项目的目的是学习并使用SPSS软件进行相关分析和回归分析，具体包括：

• 皮尔逊pearson简单相关系数的计算与分析
• 学会在SPSS上实现一元及多元回归模型的计算与检验。
• 学会回归模型的散点图与样本方程图形。
• 学会对所计算结果进行统计分析说明。
• 要求试验前，了解回归分析的如下内容。
  • 参数α、β的估计
  • 回归模型的检验方法：回归系数β的显著性检验（t－检验）；回归方程显著性检验（F－检验）。

二、试验原理

1．相关分析的统计学原理
相关分析使用某个指标来表明现象之间相互依存关系的密切程度。用来测度简单线性相关关系的系数是Pearson简单相关系数。
2．回归分析的统计学原理
相关关系不等于因果关系，要明确因果关系必须借助于回归分析。回归分析是研究两个变量或多个变量之间因果关系的统计方法。其基本思想是，在相关分析的基础上，对具有相关关系的两个或多个变量之间数量变化的一般关系进行测定，确立一个合适的数据模型，以便从一个已知量推断另一个未知量。回归分析的主要任务就是根据样本数据估计参数，建立回归模型，对参数和模型进行检验和判断，并进行预测等。
线性回归数学模型如下：

在模型中，回归系数是未知的，可以在已有样本的基础上，使用最小二乘法对回归系数进行估计，得到如下的样本回归函数：

回归模型中的参数估计出来之后，还必须对其进行检验。如果通过检验发现模型有缺陷，则必须回到模型的设定阶段或参数估计阶段，重新选择被解释变量和解释变量及其函数形式，或者对数据进行加工整理之后再次估计参数。回归模型的检验包括一级检验和二级检验。一级检验又叫统计学检验，它是利用统计学的抽样理论来检验样本回归方程的可靠性，具体又可以分为拟和优度评价和显著性检验；二级检验又称为经济计量学检验，它是对线性回归模型的假定条件能否得到满足进行检验，具体包括序列相关检验、异方差检验等。

三、试验演示内容与步骤

1．连续变量简单相关系数的计算与分析
在上市公司财务分析中，常常利用资产收益率、净资产收益率、每股净收益和托宾Q值4个指标来衡量公司经营绩效。本试验利用SPSS对这4个指标的相关性进行检验。操作步骤与过程：

• 打开数据文件“上市公司财务数据(连续变量相关分析).sav”,依次选择“【分析】→【相关】→【双变量】”打开对话框如图，将待分析的4个指标移入右边的变量列表框内。其他均可选择默认项，单击ok提交系统运行。

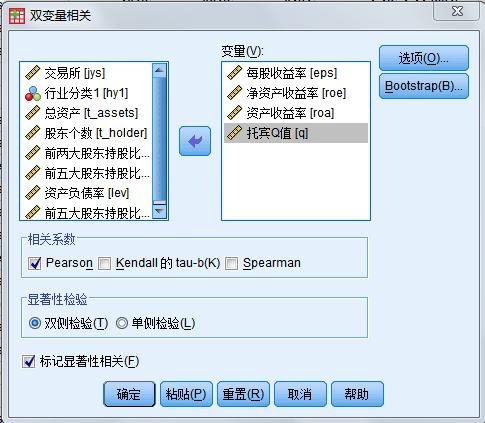
图5.1  Bivariate Correlations对话框
结果分析：
表给出了Pearson简单相关系数，相关检验t统计量对应的p值。相关系数右上角有两个星号表示相关系数在0.01的显著性水平下显著。从表中可以看出，每股收益、净资产收益率和总资产收益率3个指标之间的相关系数都在0.8以上，对应的p值都接近0，表示3个指标具有较强的正相关关系，而托宾Q值与其他3个变量之间的相关性较弱。

表5.1  Pearson简单相关分析
Correlations

**  Correlation is significant at the 0.01 level (2-tailed).
2．一元线性回归分析
实例分析：家庭住房支出与年收入的回归模型
在这个例子里，考虑家庭年收入对住房支出的影响，建立的模型如下：

其中，yi是住房支出，xi是年收入
线性回归分析的基本步骤及结果分析：
（1）绘制散点图 打开数据文件，选择【图形】-【旧对话框】-【散点/点状】，如图5.2所示。

图5.2 散点图对话框
选择简单分布，单击定义，打开子对话框，选择X变量和Y变量，如图5.3所示。单击ok提交系统运行，结果见图5.4所示。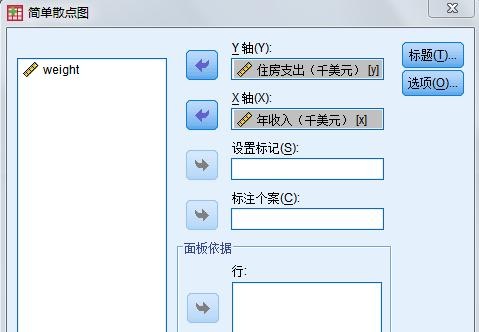

图5.3 Simple Scatterplot 子对话框
从图上可直观地看出住房支出与年收入之间存在线性相关关系。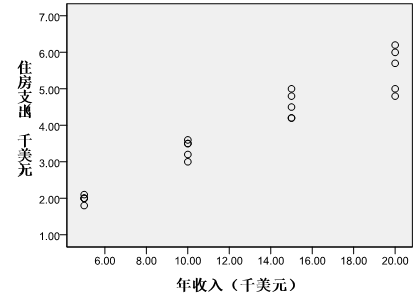

图5.4 散点图
（2）简单相关分析
选择【分析】—>【相关】—>【双变量】,打开对话框，将变量“住房支出”与“年收入”移入variables列表框，点击ok运行，结果如表5.2所示。
表5.2 住房支出与年收入相关系数表
Correlations

**  Correlation is significant at the 0.01 level (2-tailed).
从表中可得到两变量之间的皮尔逊相关系数为0.966，双尾检验概率p值尾0.000<0.05，故变量之间显著相关。根据住房支出与年收入之间的散点图与相关分析显示，住房支出与年收入之间存在显著的正相关关系。在此前提下进一步进行回归分析，建立一元线性回归方程。
(3) 线性回归分析
步骤1：选择菜单“【分析】—>【回归】—>【线性】”，打开Linear Regression 对话框。将变量住房支出y移入Dependent列表框中，将年收入x移入Independents列表框中。在Method 框中选择Enter 选项，表示所选自变量全部进入回归模型。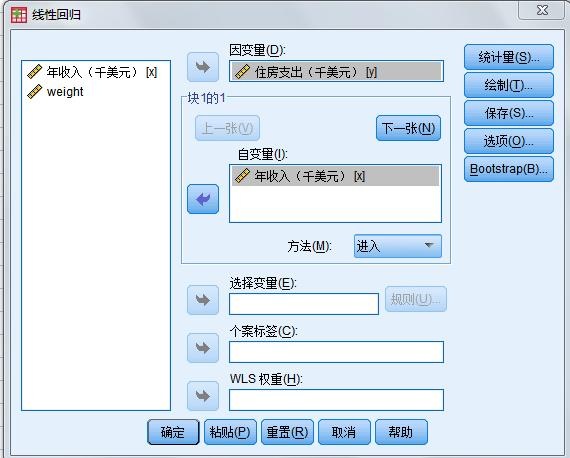

图5.5 Linear Regresssion对话框
步骤2：单击Statistics按钮，如图在Statistics子对话框。该对话框中设置要输出的统计量。这里选中估计、模型拟合度复选框。

图5.6 Statistics子对话框

• 估计：输出有关回归系数的统计量，包括回归系数、回归系数的标准差、标准化的回归系数、t统计量及其对应的p值等。
• 置信区间：输出每个回归系数的95％的置信度估计区间。
• 协方差矩阵：输出解释变量的相关系数矩阵和协差阵。
• 模型拟合度：输出可决系数、调整的可决系数、回归方程的标准误差、回归方程F检验的方差分析。

步骤3：单击绘制按钮，在Plots子对话框中的标准化残差图选项栏中选中正态概率图复选框，以便对残差的正态性进行分析。

图5.7 plots子对话框
步骤4：单击保存按钮，在Save子对话框中残差选项栏中选中未标准化复选框，这样可以在数据文件中生成一个变量名尾res_1 的残差变量，以便对残差进行进一步分析。

图5.8 Save子对话框
其余保持Spss默认选项。在主对话框中单击ok按钮，执行线性回归命令，其结果如下：
表5.3给出了回归模型的拟和优度（R Square）、调整的拟和优度（Adjusted R Square）、估计标准差（Std. Error of the Estimate）以及Durbin－Watson统计量。从结果来看，回归的可决系数和调整的可决系数分别为0.934和0.93，即住房支出的90％以上的变动都可以被该模型所解释，拟和优度较高。
表5.4给出了回归模型的方差分析表，可以看到，F统计量为252.722，对应的p值为0，所以，拒绝模型整体不显著的原假设，即该模型的整体是显著的。
表5.5给出了回归系数、回归系数的标准差、标准化的回归系数值以及各个回归系数的显著性t检验。从表中可以看到无论是常数项还是解释变量x，其t统计量对应的p值都小于显著性水平0.05，因此，在0.05的显著性水平下都通过了t检验。变量x的回归系数为0.237，即年收入每增加1千美元，住房支出就增加0.237千美元。

表5.3 回归模型拟和优度评价及Durbin－Watson检验结果
Model Summary(b)

                                a  Predictors: (Constant),年收入（千美元）
b  Dependent Variable:住房支出（千美元）
表5.4 方差分析表
ANOVA(b)

        a  Predictors: (Constant), 年收入（千美元）
b  Dependent Variable: 住房支出（千美元）
表5.5 回归系数估计及其显著性检验
Coefficients(a)

a  Dependent Variable: 住房支出（千美元）
为了判断随机扰动项是否服从正态分布，观察图5.9所示的标准化残差的P－P图，可以发现，各观测的散点基本上都分布在对角线上，据此可以初步判断残差服从正态分布。
为了判断随机扰动项是否存在异方差，根据被解释变量y与解释变量x的散点图，如图5.4所示，从图中可以看到，随着解释变量x的增大，被解释变量的波动幅度明显增大，说明随机扰动项可能存在比较严重的异方差问题，应该利用加权最小二乘法等方法对模型进行修正。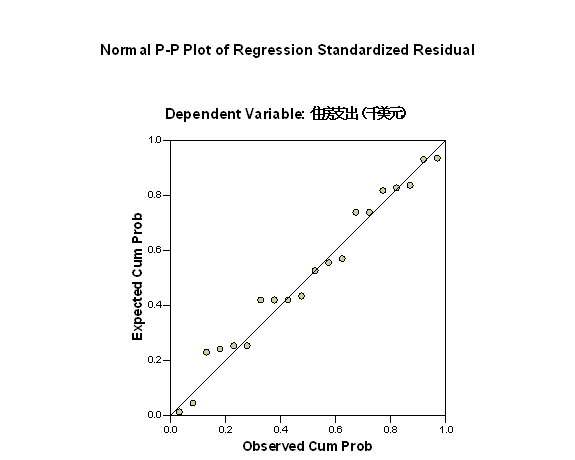

图5.9 标准化残差的P－P图

四、备择试验

现有1987~2003年湖南省全社会固定资产投资总额NINV和GDP两个指标的年度数据，见下表。试研究全社会固定资产投资总额和GDP的数量关系，并建立全社会固定资产投资总额和GDP之间的线性回归方程。
湖南省全社会固定资产投资和GDP年度数据